��Ŀ����
��֪��������y=x2-��m+1��x+m��x�ύ�ڵ�A��x1��0����B��x2��0����A��B����ࣩ����y�ύ�ڵ�C��
��1����m��1����ABC�����Ϊ6���������ߵĽ���ʽ��
��2����D��x���·����ǣ�1���е��������ϵ�һ�����㣬���ڸ������߶Գ������࣬��DE��x���������߽�����һ��E����DF��x����F����EG��x���ڵ�G�������DEGF�ܳ������ֵ��
��3����m<0����ABΪһ����x���Ϸ�������ABMN����NABΪ��ǣ��� P��AB�ߵ��е㣬Q�ǶԽ���AM��һ�㣬��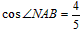 ��
��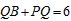 ��������ABMN��������ʱ�����A�����ꡣ
��������ABMN��������ʱ�����A�����ꡣ
��1����m��1����ABC�����Ϊ6���������ߵĽ���ʽ��
��2����D��x���·����ǣ�1���е��������ϵ�һ�����㣬���ڸ������߶Գ������࣬��DE��x���������߽�����һ��E����DF��x����F����EG��x���ڵ�G�������DEGF�ܳ������ֵ��
��3����m<0����ABΪһ����x���Ϸ�������ABMN����NABΪ��ǣ��� P��AB�ߵ��е㣬Q�ǶԽ���AM��һ�㣬��
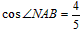 ��
��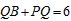 ��������ABMN��������ʱ�����A�����ꡣ
��������ABMN��������ʱ�����A�����ꡣ
�⣺�� ��������x�ύ�ڵ�A��x1��0����B��x2��0����
�� x1��x2�ǹ���x�ķ��̵�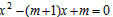 ��
��
�ⷽ�̣���x=1��x=m
��1���� A��B ����࣬m>1��
��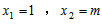 ��
��
�� AB=m-1
��������y�ύ��C��0��m����
�� OC=m
��ABC�����S=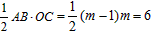
���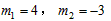 ���������⣬��ȥ��
���������⣬��ȥ��
�� �����߽���ʽΪ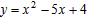
��2���� ��D�ڣ�1���е��������ϣ�
�� ��D��t��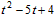 ����
����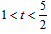 ��
��
�� F��t��0����DF=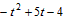
�������߶Գ�����ֱ��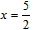 ��DE�������߶Գ��ύ���ΪR����ͼ1����
��DE�������߶Գ��ύ���ΪR����ͼ1���� 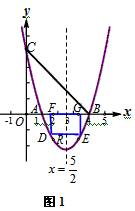
�� DR=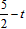 ��DE=
��DE=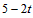 ��
��
�����DEGF���ܳ�ΪL���� L=2��DF+DE��
�� L =2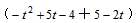
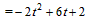
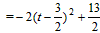
��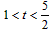 ��
��
�� ���ҽ���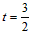 ʱ��L�����ֵ��
ʱ��L�����ֵ��
��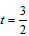 ʱ��
ʱ��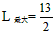
�� �����ܳ������ֵΪ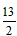
��3���� A��B ����࣬m<0��
��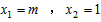 ��
��
�� AB=1-m
��ͼ2����NH��AB��H������QN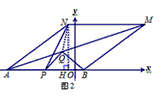
��Rt��AHN��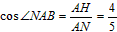
��AH=4k��k>0���� ��AN=5k��NH=3k
�� AP=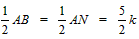 ��PH=AH-AP=
��PH=AH-AP=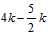 =
=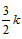 ��
��
PN=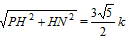
�� ����ABMN����Գ�ͼ�Σ�
�� QN=QB
�� PQ+QN=PQ+QB=6
�� PQ+QN��PN�����ҽ���P��Q��N���㹲��ʱ���Ⱥų�����
��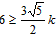 ��
��
��� k��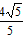
��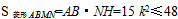
�� ���������ȡ�����ֵ48ʱ��k=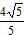
��ʱAB=5k=1-m=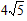
��� m=1-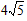
�� A���������1-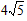 ��0����
��0����

��ϰ��ϵ�д�
�����Ŀ