题目内容
【题目】如图,已知直线 y=![]() x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在第一内作等腰 Rt△ABC,∠BAC=90. 点 P 是 x 轴上的一个动点,设 P(x,0).
x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在第一内作等腰 Rt△ABC,∠BAC=90. 点 P 是 x 轴上的一个动点,设 P(x,0).
(1)当 x =______________时,PB+PC 的值最小;
(2)当 x =______________时,|PB-PC|的值最大.

【答案】 3 -21
【解析】试题分析:(1)作点B关于x轴的对称点点B',连接B'C交x轴与点P,此时PB+PC 的值最小,作CD⊥x轴交于点D,要求点P的横坐标即要求直线B'C的解析式,即要求点B'、C的坐标,B'坐标不难求,C的坐标通过△AOB≌△CDA全等可以求得;(2)延长CB交x轴于点P,此时|PB-PC|的值最大,要求点P横坐标,即要求直线BC的解析式,求出直线BC的解析式,令y=0,求出点P的坐标即可.
试题解析:
(1)作点B关于x轴的对称点点B',连接B'C交x轴与点P,此时PB+PC 的值最小,作CD⊥x轴交于点D,
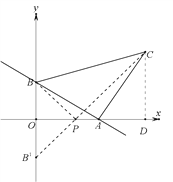
令x=0,y=3,B(0,3);令y=0,x=4,A(4,0),
∴B'(0,-3),AO=4,BO=3,
∵等腰Rt△ABC,∴∠BAC=90°,AB=AC,
∴∠BAO+∠CAD=90°,
∵∠CAD+∠ACD=90°,
∴∠BAO=∠ACD,
在△AOB和△CDA中,
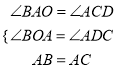 ,
,
∴△AOB≌△CDA,
∴AO=CD=4,BO=AD=3,
∴OD=7,
∴C(7, 4),
设直线B'C的解析式为:y=kx+b,
![]() ,解得
,解得![]() ,
,
∴y=x-3,
令y=0,x=3;
(2)延长CB交x轴于点P,此时|PB-PC|的值最大,
设直线BC解析式为:y=kx+b,
![]() ,解得
,解得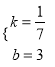 ,
,
∴y=![]() x+3,
x+3,
令y=0,x=-21.

练习册系列答案
相关题目