Question

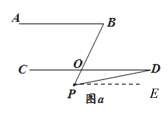
【题目】(1)如图 a，若 AB∥CD，点 P 在 AB、CD 外部，则∠BPD、∠B、∠D 之间有何数量关系？

把下面的解答填上根据：

解：∠B=∠BPD+∠PDC．

理由：作PE∥AB

∵ AB∥CD ( )

∴AB∥CD∥PE ( )

∴∠B=∠BPE， ∠D=∠DPE ( )

∵∠BPE=∠BPD+∠DPE

∴∠B=∠BPD+∠PDC ( )

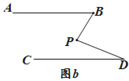
(2)若AB∥CD，将点P移到AB、CD内部，如图b，以上结论是否成立？若成立，说明理由；若不成立，则∠BPD、∠B、∠D 之间有何数量关系？请证明你的结论.

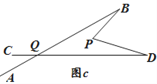
(3)在图 b 中，将直线 AB 绕点B逆时针方向旋转一定角度交直线 CD 于点 Q，如图 c，则∠BPD、∠B、∠D、∠BQD 之间满足的数量关系是 .

Answer 1

【答案】（1）答案见解析；（2）∠BPD=∠B+∠D，理由见解析；（3）∠BPD=∠B+∠D+∠BQD

【解析】试题分析：（1）∠BOD是三角形OPD的一个外角，由此可得出三个角的关系．

（2）过P作平行于AB的直线，根据内错角相等可得出三个角的关系．（3）连接BD，QP，并且延长QP交BD于E，则∠BPD=∠BPE+∠EPD=（∠PBQ+∠BQP）+（∠PDQ+∠DQP）=∠PBQ+∠PDQ+∠BQD．

试题解析：

(1)

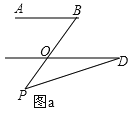
∵三角形的一个外角等于和它不相邻的两个内角的和，∴∠BOD=∠BPD+∠D.

已知；平行于同一条直线的两条直线平行；两直线平行，内错角相等；等量代换

(2)

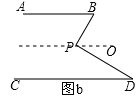
过P作平行于AB的直线PO，

∵∠BPD=∠BPO+∠OPD，∠BPO=∠B，∠OPD=∠D，

∴∠BPD=∠B+∠D.

(3)

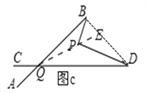
∵∠BQP+∠QBP=∠BPE，

∠DQP+∠QDP=∠DPE，

∴∠BPD=∠PBQ+∠PDQ+∠BQD.