题目内容
(1)解方程:3x2+8x-1=0(2)用配方法确定二次函数y=-2(x-1)(x+3)的图象的开口方向、对称轴和顶点坐标.
【答案】分析:(1)题由于不能用最简单的因式分解法解方程,所以最好直接用公式法解方程.
(2)题应去括号重新整理,利用配方法的基本步骤解决.
解答:解:(1)利用公式法
x=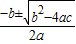 求得:
求得:
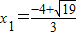 ,
,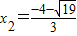
(2)y=-2(x-1)(x+3)
=-2(x2+2x-3)
=-2(x2+2x+1-4)
=-2[(x+1)2-4]
=-2(x+1)2+8
∴抛物线开口向下,对称轴是直线x=-1,顶点坐标是(-1,8)
点评:此题主要考查了公式法解方程,以及运用配方法求二次函数的顶点坐标与对称轴,这是中考中热点问题.
(2)题应去括号重新整理,利用配方法的基本步骤解决.
解答:解:(1)利用公式法
x=
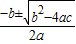 求得:
求得: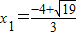 ,
,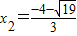
(2)y=-2(x-1)(x+3)
=-2(x2+2x-3)
=-2(x2+2x+1-4)
=-2[(x+1)2-4]
=-2(x+1)2+8
∴抛物线开口向下,对称轴是直线x=-1,顶点坐标是(-1,8)
点评:此题主要考查了公式法解方程,以及运用配方法求二次函数的顶点坐标与对称轴,这是中考中热点问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目