题目内容
【题目】综合题如图①,∠DCE=∠ECB=α,∠DAE=∠EAB=β,∠D=30°,∠B=40°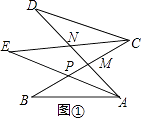
(1)①用α或β表示∠CNA,∠MPA,∠CNA= , ∠MPA=
②求∠E的大小.
(2)如图②,∠BAD的平分线AE与∠BCD的平分线CE交于点E,则∠E与∠B,∠D之间是否存在某种等量关系?若存在,写出结论,说明理由;若不存在,说明理由.
【答案】
(1)40°+α,30°+β,∵∠ECD=∠ECB= ![]() ∠BCD,∠EAD=∠EAB=
∠BCD,∠EAD=∠EAB= ![]() ∠BAD,∵∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,∴∠D+∠ECD+∠B+∠EAB=∠E+∠EAD+∠E+∠ECB∴∠D+∠B=2∠E,∴∠E=
∠BAD,∵∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,∴∠D+∠ECD+∠B+∠EAB=∠E+∠EAD+∠E+∠ECB∴∠D+∠B=2∠E,∴∠E= ![]() (∠D+∠B)=35°;
(∠D+∠B)=35°;
(2)解:延长BC交AD于点F,
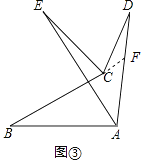
∵∠BFD=∠B+∠BAD,
∴∠BCD=∠BFD+∠D=∠B+∠BAD+∠D,
∵CE平分∠BCD,AE平分∠BAD
∴∠ECD=∠ECB= ![]() ∠BCD,∠EAD=∠EAB=
∠BCD,∠EAD=∠EAB= ![]() ∠BAD,
∠BAD,
∵∠E+∠ECB=∠B+∠EAB,
∴∠E=∠B+∠EAB﹣∠ECB=∠B+∠BAE﹣ ![]() ∠BCD=∠B+∠BAE﹣
∠BCD=∠B+∠BAE﹣ ![]() (∠B+∠BAD+∠D)=
(∠B+∠BAD+∠D)= ![]() (∠B﹣∠D),
(∠B﹣∠D),
即∠AEC= ![]() .
.
【解析】解:(1)①∠CNA=∠D+∠DCE=40°+α,∠CPA=∠B+∠BAP=30°+β,
所以答案是:40°+α,30°+β;
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角,以及对三角形的外角的理解,了解三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

【题目】2018年国家将扩大公共场所免费上网范围,某小区响应号召调查小区居民上网费用情况,随机抽查了30户家庭的月上网费用,结果如表
月网费(元) | 50 | 100 | 150 |
户数(人) | 15 | 12 | 3 |
则关于这30户家庭的月上网费用,中位数是_____.