Question

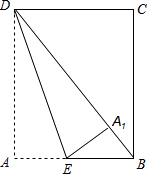
【题目】如图，在矩形纸片ABCD中，CD=12，BC=15，点E在AB上，将△DAE沿DE折叠，使点A落在对角线BD上的点A1处，求AE的长度．

Answer 1

【答案】解：∵在矩形纸片ABCD中，CD=12，BC=15， 由勾股定理求得：BD=2 ，
由折叠的性质可得：DA=DA1=BC=15，∠DA1E=∠DAE=90°，
设AE=x，则A1E=x，BE=12﹣x，BA1=2 ﹣15，
在Rt△EA1B中，（12﹣x）2=x2+（2 ﹣15）2 ，
解得：x= ，
即AE的长为 ．

【解析】由在矩形纸片ABCD中，CD=12，BC=15，利用勾股定理即可求得BD的长，然后由折叠的性质，可得DA=DA1=BC=5，∠DA1E=∠DAE=90°，再设AE=x，利用勾股定理即可得方程：（12﹣x）2=x2+82 ， 解此方程即可求得答案．
【考点精析】利用矩形的性质和翻折变换（折叠问题）对题目进行判断即可得到答案，需要熟知矩形的四个角都是直角，矩形的对角线相等；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．