Question

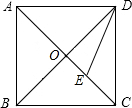如图所示，正方形ABCD的对角线AC，BD相交于点O，DE平分∠ODC交OC于点E，若AB=2，则线段OE的长为（　　）

• A、

  2

  2

• B、

  2 2

  3

• C、2-

  2

• D、

  2

  -1

Answer 1

分析：根据正方形的性质，由勾股定理得BD与AC的值，从而得到OD，OC的值，根据三角形一个角的平分线分对边所成的两条线段与这个角的两边对应成比例，OE：EC=OD：DC，从而可求得OE的长．

解答：解：∵AB=2
∴BD=AC=2

2

，OD=OC=

2

∵DE平分∠ODC交OC于点E，
∴OE：EC=OD：DC
∴OE：（

2

-OE）=

2

：2
∴OE=2-

2

故选C．

点评：本题考查了正方形的性质及角平分线的定理．