题目内容
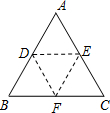 如图,将△ABC沿DE折叠,使点A与BC的中点F重合,下列结论:①EF∥AB,且EF=
如图,将△ABC沿DE折叠,使点A与BC的中点F重合,下列结论:①EF∥AB,且EF=| 1 |
| 2 |
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
分析:本题利用了:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;2、等腰三角形的判定和性质求解.
解答:解:由折叠的性质知,点A与BC的中点F重合,AD=DF,AE=EF,∠ADE=∠FDE,∠AED=∠FED,∠DAE=∠DFE,
∴△AEF,△ADF都是等腰三角形,由等腰三角形的性质:顶角的平分线与底边上的高重合知,AF⊥ED,
∴S四边形ADFE=
AF•DE正确,由三角形的外角等于与它不相邻的内角和知,∠BDF+∠FEC=2∠BAC成立,由△ADF与△AEF不一定全等,∴②∠BAF=∠CAF不一定成立,由于点D,E不一定分别是AB,AC的中点,故①EF∥AB不一定成立.故选B.
∴△AEF,△ADF都是等腰三角形,由等腰三角形的性质:顶角的平分线与底边上的高重合知,AF⊥ED,
∴S四边形ADFE=
| 1 |
| 2 |
点评:本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变.

练习册系列答案
相关题目
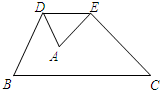 如图,将△ABC沿DE翻折,折痕DE∥BC,若
如图,将△ABC沿DE翻折,折痕DE∥BC,若| AD |
| BD |
| 1 |
| 2 |
| A、1.8 | B、2 | C、2.5 | D、3 |
 如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论正确的有( )
如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论正确的有( ) (2009•雅安)如图,将△ABC沿BC方向平移得到△A′B′C′.已知BC=
(2009•雅安)如图,将△ABC沿BC方向平移得到△A′B′C′.已知BC=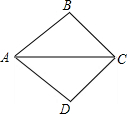 如图,将△ABC沿AC所在的直线翻折得到△ADC,且顶点B的对应顶点是D,则下列结论正确的是( )
如图,将△ABC沿AC所在的直线翻折得到△ADC,且顶点B的对应顶点是D,则下列结论正确的是( ) 如图,将△ABC沿BC方向平移1个单位得到△DEF,若△ABC的周长等于8,则四边形ABFD的周长等于( )
如图,将△ABC沿BC方向平移1个单位得到△DEF,若△ABC的周长等于8,则四边形ABFD的周长等于( )