Question

【题目】已知坐标平面内的三个点A（1，3），B（4，1），O（0，0），求△ABO的面积．

Answer 1

【答案】5.5

【解析】

试题分析：根据题意得出OC=DE=3，AC=1，CD=OE=4，BE=1，得出AD=DC﹣AC=3，BD=DE﹣BE=2，则三角形ABC的面积可以转化为矩形的面积减去三个直角三角形的面积问题，即可得出结果．

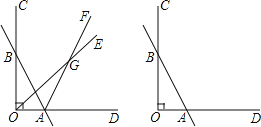
解：如图所示，则C（0，3），D（4，3），E（3，0）．

又∵O（0，0），A（1，3），B（4，1），

∴OC=DE=3，AC=1，CD=OE=4，BE=1，

∴AD=DC﹣AC=4﹣1=3，BD=DE﹣BE=3﹣1=2，

则四边形OCDE的面积=4×3=12，△ACO的面积=×3×1=1，5，△BEO的面积=×4×1=2，△ABD的面积=×3×2=3，

∴△ABO的面积=12﹣1.5﹣2﹣3=5.5．