题目内容
如图,抛物线y=ax2+bx+c的对称轴是 ,小亮通过观察得出了下面四条信息:
,小亮通过观察得出了下面四条信息:
①c<0,②abc<0,③a-b+c>0,④2a-3b=0。你认为其中正确的有____________________。(填序号)
①③.
解析试题分析:根据抛物线的开口方向,对称轴,与y轴的交点位置,x=-1时的函数值的情况,逐一判断.
试题解析:①由抛物线与y轴的交点为在y轴的负半轴上,可知c<0,正确;
②由抛物线的开口向上知,a>0,对称轴为x=?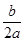 >0,a、b异号,即b<0,∴abc>0,错误;
>0,a、b异号,即b<0,∴abc>0,错误;
③当x=-1时,y=a-b+c>0,正确;
④由对称轴为x=?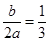 ,得2a+3b=0,错误.
,得2a+3b=0,错误.
故①③正确.
考点: 二次函数图象与系数的关系.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 ,则飞机着陆后滑行 米才能停下来。
,则飞机着陆后滑行 米才能停下来。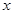 厘米,面积随之增加
厘米,面积随之增加 平方厘米,则
平方厘米,则 +bx+c的图像如图所示,则不等式ax
+bx+c的图像如图所示,则不等式ax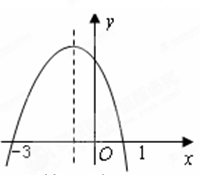

 的对称轴为
的对称轴为 ,则
,则 .
. 点表示喷水池的水面中心,
点表示喷水池的水面中心, 表示喷水柱子,水流从
表示喷水柱子,水流从 点喷出,按如图所示的直角坐标系,每一股水流在空中的路线可以用
点喷出,按如图所示的直角坐标系,每一股水流在空中的路线可以用 来描述,那么水池的半径至少要 米,才能使喷出的水流不致落到池外。
来描述,那么水池的半径至少要 米,才能使喷出的水流不致落到池外。