��Ŀ����
����Ŀ����ֱ֪��l����һ��O����A��Bͬʱ��O��������ֱ��l�Ϸֱ����������������˶�����A��B���ٶȱ�Ϊ1��2�����˶�ʱ��Ϊts��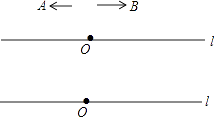
��1����t=2sʱ��AB=12cm����ʱ��
����ֱ��l�ϻ���A��B�����˶�2��ʱ��λ�ã����ش��A�˶����ٶ���cm/s�� ��B�˶����ٶ���cm/s��
������PΪֱ��l��һ�㣬��PA��PB=OP���� ![]() ��ֵ��
��ֵ��
��2���ڣ�1���������£���A��Bͬʱ��ԭ�������˶����پ������룬OA=2OB��
���𰸡�
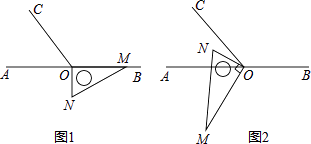
��1��2,4,�⣺��ͼ2,��P��AB֮��ʱ,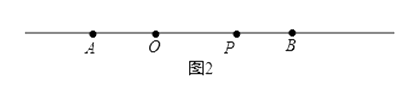 ��PA��OA=OP,PA��PB=OP,��PA��OA=PA��PB,��OA=PB=4,��OP=4����
��PA��OA=OP,PA��PB=OP,��PA��OA=PA��PB,��OA=PB=4,��OP=4���� ![]() ����ͼ3,��P��AB���Ҳ�ʱ,
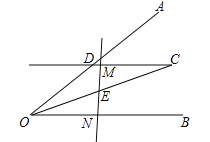
����ͼ3,��P��AB���Ҳ�ʱ, ��PA��OA=OP,PA��PB=OP, ��PA��OA=PA��PB, ��OA=PB=4,��OP=12����
��PA��OA=OP,PA��PB=OP, ��PA��OA=PA��PB, ��OA=PB=4,��OP=12���� ![]() ��
�� ![]() =
= ![]() ��1
��1
��2���⣺��A��Bͬʱ��ԭ�������˶����پ�����a��OA=2OB�������⣬��
2a+4=2��8��4a����2a+4=2��4a��8��
��ã�a= ![]() ��
�� ![]()
���پ��� ![]() ��
�� ![]() ��ʱOA=2OB��
��ʱOA=2OB��
���������⣺��1������ͼ��ʾ��
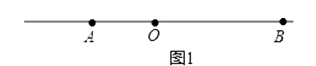
��A���ٶ�Ϊxcm/s��B���ٶ�Ϊ2xcm/s�������⣬��
2x+4x=12��
��ã�x=2��
��B���ٶ�Ϊ4cm/s��
�ʴ�Ϊ��2��4
��1������A���ٶ�Ϊxcm/s��B���ٶ�Ϊ2xcm/s������2s���ľ���Ϊ12�������������⼴�ɣ�
�ڷ����������ͼ2�� ��P��AB֮��ʱ������PA��OA=OP��PA��PB=OP ���ó�OA=PB=4�������߶εĺͲ�ó�OP=4 ���Ӷ��ó���OP��AB��ֵ����ͼ3����P��AB���Ҳ�ʱ����PA��OA=OP��PA��PB=OP���ó�OA=PB=4�������ó�OP=12 ���Ӷ��ó�OP��AB��ֵ ��
��2����A��Bͬʱ��ԭ�������˶����پ�����a��OA=2OB�������������������ϵ��������2a+4=2��8��4a����2a+4=2��4a��8�� �����⼴�ɣ�