题目内容
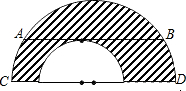如图，两个半圆，大半圆中长为12的弦AB平行于直径CD，且与小半圆相切，则图中阴影部分的面积为（ ）| A、16π | B、18π | C、32π | D、36π |
分析：设大圆圆心为F，作EF⊥AB，垂足为E，连接FA，由垂径定理知及勾股定理即可求出AF、EF的长，再根据圆的面积公式即可求出阴影部分的面积．
解答：解：设大圆圆心为F，连接FA，则FA是大圆半径，
EF的长等于小圆的半径，点E是AB的中点，FA2-EF2=AE2=36，阴影部分的面积等于大半圆面积减去小半圆面积，
∴阴影部分的面积=
（FA2-EF2）π=18π．故选B．
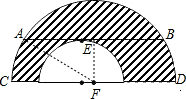
EF的长等于小圆的半径，点E是AB的中点，FA2-EF2=AE2=36，阴影部分的面积等于大半圆面积减去小半圆面积，
∴阴影部分的面积=
| 1 |
| 2 |
点评：本题利用了垂径定理和勾股定理，圆的面积公式求解．
练习册系列答案
相关题目
10、如图，大半圆中有n个小半圆，现有甲、乙两虫停留在A处，如果甲虫沿着大半圆弧爬向B处，乙虫沿着n个小半圆弧爬向B处，并且假定甲、乙两虫的爬行速度相同，那么下列说法正确的是（ ）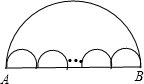
如图，大半圆中有n个小半圆，现有甲、乙两虫停留在A处，如果甲虫沿着大半圆弧爬向B处，乙虫沿着n个小半圆弧爬向B处，并且假定甲、乙两虫的爬行速度相同，那么下列说法正确的是