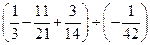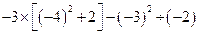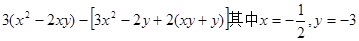题目内容
如果多项式3x3-2x2+x+│k│x2-5中不含x2项,则k的值为( ).
| A.±2 | B.-2 | C.2 | D.0 |
A
要使3x3-2x2+x+|k|x2-5中不含x2项,那么x2项的系数应为0.在多项式3x3-2x2+x+|k|x2-5中-2x2和|k|x2两项含x2,在合并同类项时这两项的系数和0,由此可以得到关于k的方程,解方程即可求出k.
解:要使3x3-2x2+x+|k|x2-5中不含x2项,那么x2项的系数应为0,
在多项式3x3-2x2+x+|k|x2-5中-2x2和|k|x2两项含x2,
∴在合并同类项时这两项的系数互为相反数,结果为0,
即-2=-|k|,
∴k=±2.
故选A.
点评:在多项式中如果不含哪一项,即哪项的系数为0,即这些项的系数和为0.
解:要使3x3-2x2+x+|k|x2-5中不含x2项,那么x2项的系数应为0,
在多项式3x3-2x2+x+|k|x2-5中-2x2和|k|x2两项含x2,
∴在合并同类项时这两项的系数互为相反数,结果为0,
即-2=-|k|,
∴k=±2.
故选A.
点评:在多项式中如果不含哪一项,即哪项的系数为0,即这些项的系数和为0.

练习册系列答案
相关题目
 ,
,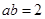 ,则
,则 ___________
___________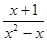 -
-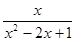 )÷
)÷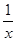 ,然后请选取一个你最喜欢的x值代入求出这个式子的值.
,然后请选取一个你最喜欢的x值代入求出这个式子的值.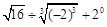 ②
② 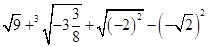
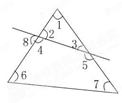
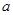 桶水,七年级二班本学期用了
桶水,七年级二班本学期用了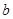 桶水,则本期两个班共需交水费 元.
桶水,则本期两个班共需交水费 元. (2)
(2)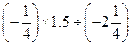 (3)
(3)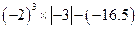 (4)
(4)