题目内容
【题目】如图，在菱形ABCD中，∠BAD=60°，M为对角线BD延长线上一点，连接AM和CM，E为CM上一点，且满足CB=CE，连接BE，交CD于点F．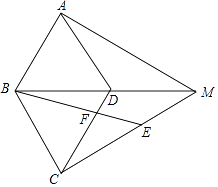
（1）若∠AMB=30°，且DM=3，求BE的长；
（2）证明：AM=CF+DM．
【答案】
（1）解：如图1中，
∵四边形ABCD是菱形，∠BAD=60°，
∴△ABD，△BCD的是等边三角形，
∴∠ABD=∠CBD=∠ADB=∠BAD=60°，BA=BC，
∵∠AMB=30°，∠ADB=∠AMB+∠DAM，
∴∠DAM=∠DMA=30°，
∴∠BAM=90°，DA=DM=AB=BC=CE=3，
在△BMA和△BMC中，
，
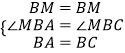∴△BMA≌△BMC，
∴∠BCM=∠BAM=90°，
在Rt△BCE中，BE= 
=3 
．
（2）解：如图2中，在BD上取一点G，使得BG=DF，连接CG交BE于O．
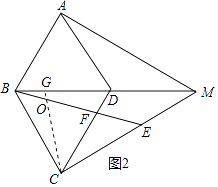
∵BG=DF，∠CBG=∠BDF，BD=BC，
∴△GBC≌△FDB，
∴∠BGC=∠BFD，∠DBF=∠BCG，
∴∠MGC=∠BFC，
∵∠COF=∠CBO+∠OCB=∠CBO+∠DBF=60°
在△COE中，∠ECO+∠EOC+∠CEO=180°，
在△BCF中，∠BFC+∠CBF+∠BCF=180°，
∵CB=CE，
∴∠CBE=∠CEO，∵∠BCF=∠COE=60°，
∴∠ECO=∠BFC=∠MGC，
∴MC=MG，
由（1）可知△BMA≌△BMC，
∴AM=MC=MG，
∵MG=DG+DM，
∵BD=CD，BG=DF，
∴DG=CF，
∴AM=CF+DM
【解析】（1）根据菱形的性质和全等三角形的性质可得出△BCE是等腰直角三角形，即可求出BE的长；（2）证两线段之和等于一条线段可采取“截长补短法“，即在长线段BM上截取BG=DF，构造全等三角形△GBC≌△FDB，可推出CF=DG，再结合已知AM=CM=MG，得出结论.
【考点精析】根据题目的已知条件，利用菱形的性质的相关知识可以得到问题的答案，需要掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．
