题目内容
【题目】如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是_____.
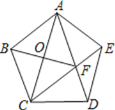
【答案】AC2+BF2=4CD2
【解析】
首先根据菱形的判定方法,判断出四边形ABCF是菱形,再根据菱形的性质,即可判断出AC⊥BF;然后根据勾股定理,可得OB2+OC2=BC2,据此推得AC2+BF2=4CD2即可.
解:∵五边形ABCDE是正五边形,
∴AB∥CE,AD∥BC,
∴四边形ABCF是平行四边形,
又∵AB=BC=CD=DE=EA,
∴四边形ABCF是菱形,
∴AC⊥BF,
∴OB2+OC2=BC2,
∵AC=2OC,BF=2OB,
∴AC2+BF2=(2OC)2+(2OB)2=4OC2+4OB2=4BC2,
又∵BC=CD,
∴AC2+BF2=4CD2.
故答案为:AC2+BF2=4CD2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目