题目内容
(10分)
如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.

⑴请判断四边形EFGH的形状?并说明为什么.
⑵若使四边形EFGH为正方形,那么四边形ABCD的对角线应具有怎样的性质?
如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.

⑴请判断四边形EFGH的形状?并说明为什么.
⑵若使四边形EFGH为正方形,那么四边形ABCD的对角线应具有怎样的性质?
略
分析(1)连接四边形的对角线,根据题目所给四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,可得四边形对边平行且相等,从而判断平行四边形;
(2)只要加对角线相等且互相垂直就可证明是正方形;
解:(1)∵E是AB的中点,H是AD的中点,
∴EH∥BD,EH="1/2" BD
∵F是BC的中点,G是CD的中点
∴GF∥BD,GF="1/2" BD
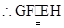
∴四边形EFGH是平行四边形.
(2)若加AC=BD且AC⊥BD,则四边形EFGH会是正方形
在(1)的条件下,∵AC=BD
∴EF=FG=GH=HE
∴四边形EFGH是菱形.
又∵AC⊥BD,EH∥BD,EF∥AC
∴∠HEF=90°
∴四边形EFGH是正方形

练习册系列答案
相关题目
 的大小(菱形的边长不变),从而改变千斤顶的高度(即A、C之间的距离).若AB=40cm,当
的大小(菱形的边长不变),从而改变千斤顶的高度(即A、C之间的距离).若AB=40cm,当 变为
变为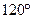 时,千斤顶升高了多少?
时,千斤顶升高了多少?





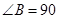 °。以边AC上的点O为圆心、OA为半径的⊙O与EC相切,D为切点,AD//BC。
°。以边AC上的点O为圆心、OA为半径的⊙O与EC相切,D为切点,AD//BC。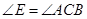
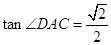 ,求BC的长。(8分)
,求BC的长。(8分) ??
??