题目内容
在平面直角坐标系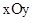 中,二次函数
中,二次函数 (
( )的图象与
)的图象与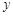 轴正半轴交于A点.
轴正半轴交于A点.
(1)求证:该二次函数的图象与x轴必有两个交点;
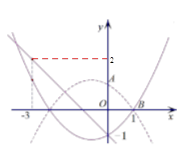
(2)设该二次函数的图象与x轴的两个交点中右侧的交点为点B,若∠ABO=45°,将直线AB向下平移2个单位得到直线l,求直线l的解析式;
(3)在(2)的条件下,设M(p,q)为二次函数图象上的一个动点,当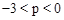 时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.

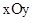 中,二次函数
中,二次函数 (
( )的图象与
)的图象与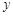 轴正半轴交于A点.
轴正半轴交于A点.(1)求证:该二次函数的图象与x轴必有两个交点;
(2)设该二次函数的图象与x轴的两个交点中右侧的交点为点B,若∠ABO=45°,将直线AB向下平移2个单位得到直线l,求直线l的解析式;
(3)在(2)的条件下,设M(p,q)为二次函数图象上的一个动点,当
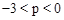 时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
(1)证明见解析;(2)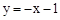 ;(3)
;(3)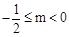 .
.
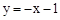 ;(3)
;(3)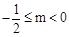 .
.试题分析:(1)根据二次函数与一元二次方程的关系,要证明二次函数的图象与x轴有两个交点,只要对应的一元二次方程根的判别式大于0即可.
(2)求出直线AB的解析式,根据平移的性质即可得直线l的解析式.
(3)求出点M关于x轴的对称点
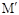 所在的二次函数解析式,由其在直线l的下方求出m的取值范围.
所在的二次函数解析式,由其在直线l的下方求出m的取值范围.试题解析:(1)令
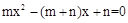 ,则
,则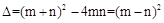 .
.∵二次函数图象与y轴正半轴交于A点,
∴
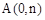 ,且
,且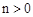 .
.又
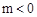 ,∴
,∴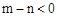 .
.∴
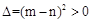 .
.∴该二次函数的图象与x轴必有两个交点.
(2)令
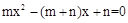 ,解得:
,解得: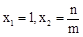 .
.由(1)得
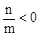 ,故B的坐标为(1,0).
,故B的坐标为(1,0).又因为∠ABO=45°,所以
 ,即
,即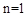 .
.则可求得直线AB的解析式为
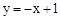 .
.再向下平移2个单位可得到直线
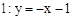 .
.(3)由(2)得二次函数的解析式为
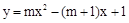
∵M(p,q)为二次函数图象上的一个动点,
∴
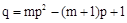 .
.∴点M关于x轴的对称点
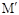 的坐标为
的坐标为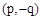 .
.∴点
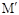 在二次函数
在二次函数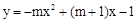 上.
上.∵当
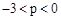 时,点M关于x轴的对称点都在直线l的下方,
时,点M关于x轴的对称点都在直线l的下方,当
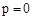 时,
时,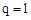 ;当
;当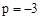 时,
时,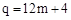 .
.结合图象可知:
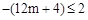 ,
,解得:
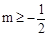 .
.∴
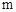 的取值范围为
的取值范围为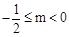 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
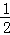 x2对应的碟宽为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ;
x2对应的碟宽为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ; (a>0)对应的碟宽为6,且在x轴上,求a的值;
(a>0)对应的碟宽为6,且在x轴上,求a的值;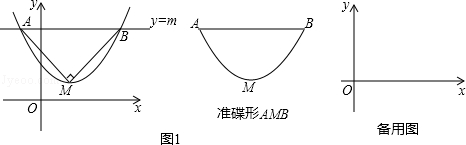
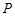 的横坐标,将它所对的面的数字作为点
的横坐标,将它所对的面的数字作为点 与
与 轴所围成的区域内(不含边界)的概率是 .
轴所围成的区域内(不含边界)的概率是 . 表示,例如图1中,
表示,例如图1中, ,图2中,
,图2中, .
. ,
, ,
, )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2, ,则
,则 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标” 为
为 .在图3中,我们知道
.在图3中,我们知道 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: .
. ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现: 中,点
中,点 ,
, 的“面积坐标”为
的“面积坐标”为 ,
, 与
与 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;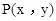 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于 ,点Q在抛物线
,点Q在抛物线 上,求当
上,求当 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.



 的顶点坐标为 .
的顶点坐标为 .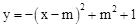 有最大值4,则实数m的值为( )
有最大值4,则实数m的值为( )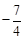 (B)
(B)  或
或 (c)2或
(c)2或