题目内容
(2002•哈尔滨)解方程: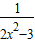 -8x2+12=0
-8x2+12=0
【答案】分析:当分式方程比较复杂时,通常采用换元法使分式方程简化,可设y=2x2-3.
解答:解:原方程化为 =0
=0
设2x2-3=y.(1分)
于是原方程变形为
方程的两边都乘以y,约去分母,得1-4y2=0.
解这个方程,得 ,
, (2分)
(2分)
当y= 时,2x2-3=
时,2x2-3= 解这个方程,得x=±
解这个方程,得x=± (3分)
(3分)
当y=- 时,2x2-3=-
时,2x2-3=- ,解这个方程得x=±
,解这个方程得x=± .(4分)
.(4分)
检验:把x=± ,x=±
,x=± 分别代入原方程的分母,各分母都不等于0,所以他们都是原方程的根.(5分)
分别代入原方程的分母,各分母都不等于0,所以他们都是原方程的根.(5分)
∴原方程的根是 ,
, ,
, ,
, .(6分)
.(6分)
点评:当分式方程比较复杂时,通常采用换元法使分式方程简化.解分式方程一定注意要代入最简公分母验根.
解答:解:原方程化为
 =0
=0设2x2-3=y.(1分)
于是原方程变形为

方程的两边都乘以y,约去分母,得1-4y2=0.
解这个方程,得
 ,
, (2分)
(2分)当y=
 时,2x2-3=
时,2x2-3= 解这个方程,得x=±
解这个方程,得x=± (3分)
(3分)当y=-
 时,2x2-3=-
时,2x2-3=- ,解这个方程得x=±
,解这个方程得x=± .(4分)
.(4分)检验:把x=±
 ,x=±
,x=± 分别代入原方程的分母,各分母都不等于0,所以他们都是原方程的根.(5分)
分别代入原方程的分母,各分母都不等于0,所以他们都是原方程的根.(5分)∴原方程的根是
 ,
, ,
, ,
, .(6分)
.(6分)点评:当分式方程比较复杂时,通常采用换元法使分式方程简化.解分式方程一定注意要代入最简公分母验根.

练习册系列答案
相关题目


