题目内容
【题目】如图，四边形ABCD中，AD∥BC，DE平分∠ADB，∠BDC=∠BCD，
（1）求证：∠1+∠2＝90°.
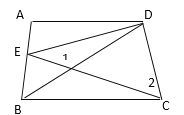
（2）若∠ABD的平分线与CD的延长线交于F，且∠F=55°，求∠ABC.
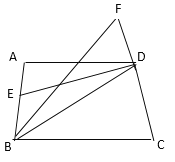
【答案】（1）见解析；(2)70°.
【解析】
（1）由AD//BC，DE平分∠ADB，得∠ADC+∠BCD=180°，∠BDC=∠BCD，得出∠1+∠2=90°；
（2）由DE平分∠ADB，CD平分∠ABD，四边形ABCD中，AD//BC，∠F=55°，得出∠ABC=∠ABD+∠DBC=∠ABD+∠ADB，即∠ABC=70°；
（1）证明：∵AD//BC
∴∠ADC+∠BCD=180°
∵DE平分∠ADB
∴∠BDC=∠BCD
∴∠ADE=∠EDB
∵∠ADC+∠BCD=180°
∴∠EDB+∠BDC=90°=∠1+∠2=90°
解：（2）∠FBD+∠BDE=90°-∠F=35°
∵DE平分∠ADB，BF平分∠ABD
∴. ∠ADB+∠ABD=2（∠FBD+∠BDE）=70°
又∵四边形ABCD中，AD//BC
∴∠DBC=∠ADB
∴∠ABC=∠ABD+∠DBC=∠ABD+∠ADB =70°；
练习册系列答案
相关题目
【题目】某烤鸭店在确定烤鸭的烤制时间时，主要依据的是下表的数据：
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为
千克，烤制时间为
，估计当
千克时，的值为（ ）
A.138B.140C.148D.160
