题目内容
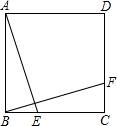
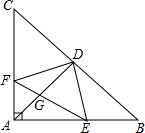
如图,在等腰直角三角形ABC中,AD为斜边上的高,点E、F分别在AB、AC上,△AED经过旋转到了△CFD的位置.
(1)△BED和△AFD之间可以看成是经过怎样的变换得到的?
(2)AD与EF相交于点G,试判断∠AED与∠AGF的大小关系,并说明理由.
(1)△BED和△AFD之间可以看成是经过怎样的变换得到的?
(2)AD与EF相交于点G,试判断∠AED与∠AGF的大小关系,并说明理由.

(1)∵△AED经过旋转到了△CFD的位置,
∴DE=DF,AD=CD,
∵在等腰直角三角形ABC中,AD为斜边上的高,
∴AD=AD=BD,∠ADC=∠CDB=90°,
∴∠EDF=90°,
∴△AFD可以看成是△BED绕点D按顺时针方向旋转90°得到的;
(2)∠AED=∠AGF.
理由:∵DF=DE,∠FDE=90°,
∴∠DFE=∠DEF=45°,
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD=45°,
∵∠AGF=∠DAE+∠AEG=45°+∠AEG,
∠AED=∠DEF+∠AEF=45°+∠AEG,
∴∠AED=∠AGF.

∴DE=DF,AD=CD,
∵在等腰直角三角形ABC中,AD为斜边上的高,
∴AD=AD=BD,∠ADC=∠CDB=90°,
∴∠EDF=90°,
∴△AFD可以看成是△BED绕点D按顺时针方向旋转90°得到的;
(2)∠AED=∠AGF.
理由:∵DF=DE,∠FDE=90°,
∴∠DFE=∠DEF=45°,
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD=45°,
∵∠AGF=∠DAE+∠AEG=45°+∠AEG,
∠AED=∠DEF+∠AEF=45°+∠AEG,
∴∠AED=∠AGF.


练习册系列答案
相关题目
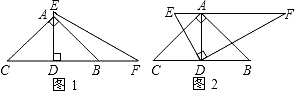 系?为什么?
系?为什么?