题目内容
若多项式2x3-10x2+20x除以ax+b,得商式为x2+10,余式为100,则
之值为何?( )
| b |
| a |
| A、0 | B、-5 | C、-10 | D、-15 |
分析:根据被除式=除式×商式+余式计算即可.
解答:解:由题意可知,可整除(2x3-10x2+20x)÷(ax+b)=x2+10…100,
整理得:2x3-10x2+20x=ax3+110ax+bx2+110b,
∴a=2,b=-10,
∴
=
=-5,
故选B.
整理得:2x3-10x2+20x=ax3+110ax+bx2+110b,
∴a=2,b=-10,
∴
| b |
| a |
| -10 |
| 2 |
故选B.
点评:本题考查了整式的除法,用到的知识点:被除式=除式×商式+余式.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 之值为何?
之值为何?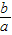 之值为何?( )
之值为何?( )