题目内容
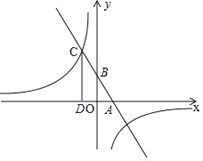
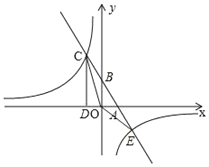
【题目】已知,如图,一次函数y=kx+b(k、b为常数且k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() ,m为常数且m≠0)的图象在第二象限交于点C.若CD⊥x轴于D,若OA=OD=2,cos∠BAO=
,m为常数且m≠0)的图象在第二象限交于点C.若CD⊥x轴于D,若OA=OD=2,cos∠BAO=![]() .
.
(1)求一次函数与反比例函数的解析式.
(2)若一次函数与反比例函数的另一个交点坐标为E,连接OC、OE,求△COE面积.
【答案】(1)y=-![]() ,y=﹣
,y=﹣![]() x+3(2)9
x+3(2)9
【解析】
(1)根据OA=OD=2,cos∠BAO=![]() 和勾股定理,求得C(﹣2,6),把C(﹣2,6)代入反比例函数y=
和勾股定理,求得C(﹣2,6),把C(﹣2,6)代入反比例函数y=![]() ,可得反比例函数的解析式,把C(﹣2,6),A(2,0)代入一次函数y=kx+b,即可得一次函数解析式;
,可得反比例函数的解析式,把C(﹣2,6),A(2,0)代入一次函数y=kx+b,即可得一次函数解析式;
(2)先求得一次函数与y轴的B的坐标,再根据反比例函数的解析式和一次函数解析式求出交点E的坐标,再根据S△COE=S△COB+S△EOB进行计算即可.
(1)在Rt△ACD中,
∵OA=OD=2,cos∠BAO=![]() =
=![]() ,
,
∴AC=2![]() ,AD=4,
,AD=4,
∴Rt△ACD中,CD=![]() =6,
=6,
∴C(﹣2,6),
把C(﹣2,6)代入反比例函数y=![]() ,可得
,可得
m=﹣12,
∴反比例函数的解析式为y=﹣![]() .
.
把C(﹣2,6),A(2,0)代入一次函数y=kx+b,
可得![]() ,解得
,解得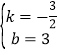
∴一次函数解析式为y=﹣![]() x+3;
x+3;
(2)y=﹣![]() x+3中,令x=0,则y=3,即B(0,3),
x+3中,令x=0,则y=3,即B(0,3),
解方程组 ,可得
,可得![]() ,
,![]() ,
,
∴E(4,﹣3),
∴S△COE=S△COB+S△EOB
=![]() ×3×(2+4)
×3×(2+4)
=9.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目