题目内容
(2012•厦门)已知点A(1,c)和点B(3,d)是直线y=k1x+b与双曲线y=
(k2>0)的交点.
(1)过点A作AM⊥x轴,垂足为M,连接BM.若AM=BM,求点B的坐标.
(2)若点P在线段AB上,过点P作PE⊥x轴,垂足为E,并交双曲线y=
(k2>0)于点N.当
取最大值时,有PN=
,求此时双曲线的解析式.
| k2 |
| x |
(1)过点A作AM⊥x轴,垂足为M,连接BM.若AM=BM,求点B的坐标.
(2)若点P在线段AB上,过点P作PE⊥x轴,垂足为E,并交双曲线y=
| k2 |
| x |
| PN |
| NE |
| 1 |
| 2 |
分析:(1)过B作BN⊥x轴,由点A(1,c)和点B(3,d)都在双曲线y=
(k2>0)上,得到即c=3d,则A点坐标为(1,3d),根据勾股定理计算出MB=
,然后利用AM=BM得到(3d)2=22+d2,求出d的值,即可确定B点坐标;
(2)由B(3,d)可得到反比例函数的解析式为y=
,然后利用待定系数法求出直线AB的解析式为y=-dx+4d,则可设P(t,-dt+4d),则N(t,
),表示出PN=-dt+4d-
,NE=
,再计算
=
=-
t2+
t-1,配方得-
(t-2)2+
,由于
取最大值,所以t=2,此时PN=-dt+4d-
=
,解方程得到d的值,即可确定双曲线的解析式.
| k2 |
| x |
| 22+d2 |
(2)由B(3,d)可得到反比例函数的解析式为y=
| 3d |
| x |
| 3d |
| t |
| 3d |
| t |
| 3d |
| t |
| PN |
| NE |
-dt+4d-
| ||
|
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| PN |
| NE |
| 3d |
| t |
| 1 |
| 2 |
解答:解:(1)如图,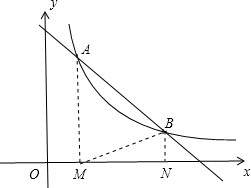 过B作BN⊥x轴,
过B作BN⊥x轴,
∵点A(1,c)和点B(3,d)都在双曲线y=
(k2>0)上,
∴1×c=3×d,即c=3d,
∴A点坐标为(1,3d),
∴AM=3d,
∵MN=3-1=2,BN=d,
∴MB=
,
而AM=BM,
∴(3d)2=22+d2,
∴d=
,
∴B点坐标为(3,
);
(2)如图,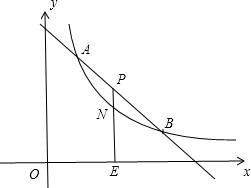 把B(3,d)代入y=
把B(3,d)代入y=
得k2=3d,
∴反比例函数的解析式为y=
,
把A(1,3d)、B(3,d)代入y=k1x+b得,
,解得
,
∴直线AB的解析式为y=-dx+4d,
设P(t,-dt+4d),则N(t,
),
∴PN=-dt+4d-
,NE=
,
∴
=
=-
t2+
t-1=-
(t-2)2+
,
当
取最大值时,t=2,
此时PN=-dt+4d-
=
,
∴-2d+4d-
=
,
∴d=1,
∴反比例函数的解析式为y=
.
 过B作BN⊥x轴,
过B作BN⊥x轴,∵点A(1,c)和点B(3,d)都在双曲线y=
| k2 |
| x |
∴1×c=3×d,即c=3d,
∴A点坐标为(1,3d),
∴AM=3d,
∵MN=3-1=2,BN=d,
∴MB=
| 22+d2 |
而AM=BM,
∴(3d)2=22+d2,
∴d=
| ||
| 2 |
∴B点坐标为(3,
| ||
| 2 |
(2)如图,
 把B(3,d)代入y=
把B(3,d)代入y=| k2 |
| x |
∴反比例函数的解析式为y=
| 3d |
| x |
把A(1,3d)、B(3,d)代入y=k1x+b得,
|
|
∴直线AB的解析式为y=-dx+4d,
设P(t,-dt+4d),则N(t,
| 3d |
| t |
∴PN=-dt+4d-
| 3d |
| t |
| 3d |
| t |
∴
| PN |
| NE |
-dt+4d-
| ||
|
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
当
| PN |
| NE |
此时PN=-dt+4d-
| 3d |
| t |
| 1 |
| 2 |
∴-2d+4d-
| 3d |
| 2 |
| 1 |
| 2 |
∴d=1,
∴反比例函数的解析式为y=
| 3 |
| x |
点评:本题考查了反比例函数综合题:点在函数图象上,则点的横纵坐标满足其解析式;运用待定系数法求函数的解析式;利用配方法讨论确定最值问题以及勾股定理计算有关线段的长度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•厦门)已知:如图,在△ABC中,∠C=90°,点D、E分别在边AB、AC上,DE∥BC,DE=3,BC=9
(2012•厦门)已知:如图,在△ABC中,∠C=90°,点D、E分别在边AB、AC上,DE∥BC,DE=3,BC=9 (2012•厦门)已知:⊙O是△ABC的外接圆,AB为⊙O的直径,弦CD交AB于E,∠BCD=∠BAC.
(2012•厦门)已知:⊙O是△ABC的外接圆,AB为⊙O的直径,弦CD交AB于E,∠BCD=∠BAC.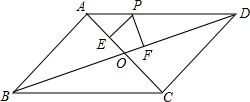 (2012•厦门)已知平行四边形ABCD,对角线AC和BD相交于点O,点P在边AD上,过点P作PE⊥AC,PF⊥BD,垂足分别为E、F,PE=PF.
(2012•厦门)已知平行四边形ABCD,对角线AC和BD相交于点O,点P在边AD上,过点P作PE⊥AC,PF⊥BD,垂足分别为E、F,PE=PF.