题目内容
 (2012•厦门)已知:⊙O是△ABC的外接圆,AB为⊙O的直径,弦CD交AB于E,∠BCD=∠BAC.
(2012•厦门)已知:⊙O是△ABC的外接圆,AB为⊙O的直径,弦CD交AB于E,∠BCD=∠BAC.(1)求证:AC=AD;
(2)过点C作直线CF,交AB的延长线于点F,若∠BCF=30°,则结论“CF一定是⊙O的切线”是否正确?若正确,请证明;若不正确,请举反例.
分析:(1)连接AD.根据∠BCD=∠BAC,∠CBE=∠ABC,证出△CBE∽△ABC,可得∠BEC=90°,于是∠D=∠CBA=∠ACD,故AC=AD.
(2)连接OC,不正确,可令∠CAB=20°,据此推出∠OCF≠90°,从而证出∠BCF=30°时“CF不一定是⊙O的切线”.
(2)连接OC,不正确,可令∠CAB=20°,据此推出∠OCF≠90°,从而证出∠BCF=30°时“CF不一定是⊙O的切线”.
解答: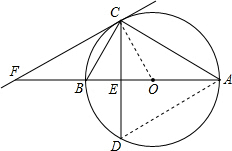 证明:(1)连接AD,
证明:(1)连接AD,
∵∠BCD=∠BAC,∠CBE=∠ABC,
∴△CBE∽△ABC,
∴∠BEC=∠BCA=90°,
∴∠CBA=∠ECA,
又∵∠D=∠ABC,
∴∠D=∠ACD,
∴AC=AD.
(2)连接OC,令∠CAB=20°,
∵OA=OC,
∴∠ACO=∠CAB=20°,
∴∠COB=20°+20°=40°,
∴∠OCB=
(180°-40°)=70°,
∴∠FCO=∠FCB+∠OCB=70°+30°=100°,
故此时FC不是⊙O的切线.
同理,当∠CAB=50°时,FC不一定是⊙O的切线.
 证明:(1)连接AD,
证明:(1)连接AD,∵∠BCD=∠BAC,∠CBE=∠ABC,
∴△CBE∽△ABC,
∴∠BEC=∠BCA=90°,
∴∠CBA=∠ECA,
又∵∠D=∠ABC,
∴∠D=∠ACD,
∴AC=AD.
(2)连接OC,令∠CAB=20°,
∵OA=OC,
∴∠ACO=∠CAB=20°,
∴∠COB=20°+20°=40°,
∴∠OCB=
| 1 |
| 2 |
∴∠FCO=∠FCB+∠OCB=70°+30°=100°,
故此时FC不是⊙O的切线.
同理,当∠CAB=50°时,FC不一定是⊙O的切线.
点评:本题考查了切线的判定、垂径定理、圆周角定理,作出辅助线OC、AD是解题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
 (2012•厦门)已知:如图,在△ABC中,∠C=90°,点D、E分别在边AB、AC上,DE∥BC,DE=3,BC=9
(2012•厦门)已知:如图,在△ABC中,∠C=90°,点D、E分别在边AB、AC上,DE∥BC,DE=3,BC=9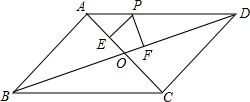 (2012•厦门)已知平行四边形ABCD,对角线AC和BD相交于点O,点P在边AD上,过点P作PE⊥AC,PF⊥BD,垂足分别为E、F,PE=PF.
(2012•厦门)已知平行四边形ABCD,对角线AC和BD相交于点O,点P在边AD上,过点P作PE⊥AC,PF⊥BD,垂足分别为E、F,PE=PF.