题目内容
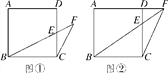
【题目】已知正方形ABCD,点E在边CD上,点F在线段BE的延长线上,连接FC,且∠FCE=∠CBE.
(1)如图①,当点E为CD边的中点时,求证:CF=2EF;
(2)如图②,当点F位于线段AD的延长线上时,求证: ![]() .
.
【答案】(1)见解析 (2)见解析
证明:(1)∵四边形ABCD是正方形,
∴CD=BC.∵点E为CD边的中点,
∴CE=![]() CD=
CD=![]() BC.
BC.
∵∠FCE=∠CBE,∠F=∠F,∴△FCE∽△FBC,
∴![]()
又∵CE=![]() BC,∴
BC,∴![]() =
=![]() ,∴CF=2EF.
,∴CF=2EF.
(2)∵四边形ABCD是正方形,∴DE∥AB,AD∥BC,AD=CD,∴ ![]() =
=![]() ,
,
∴![]() =
=![]() .∵AF∥BC,∴∠DFE=∠CBE.∵∠FCE=∠CBE,∴∠DFE=∠FCE.又∵∠FDE=∠CDF,∴△FDE∽△CDF,∴
.∵AF∥BC,∴∠DFE=∠CBE.∵∠FCE=∠CBE,∴∠DFE=∠FCE.又∵∠FDE=∠CDF,∴△FDE∽△CDF,∴![]() =
=![]() ,∴
,∴![]() =
=![]() .
.
【解析】试题分析:根据正方形的性质得到![]() ,由点
,由点![]() 为
为![]() 边的中点,得到
边的中点,得到![]() 根据相似三角形的性质即可得到结论;
根据相似三角形的性质即可得到结论;
![]() 根据正方形的性质得到
根据正方形的性质得到![]() 根据平行线分线段成比例定理得到
根据平行线分线段成比例定理得到![]() 等量代换得到
等量代换得到![]() 根据相似三角形的性质得到
根据相似三角形的性质得到![]()
于是得到结论.
试题解析:(1)∵四边形ABCD是正方形,
∴CD=BC.
∵点E为CD边的中点,
![]()
∵∠FCE=∠CBE,∠F=∠F,
∴△FCE∽△FBC,
![]()
又∵![]()
![]()
∴CF=2EF.
(2)∵四边形ABCD是正方形,
∴DE∥AB,AD∥BC,AD=CD,
![]()
![]()
∵AF∥BC,
∴∠DFE=∠CBE.
∵∠FCE=∠CBE,
∴∠DFE=∠FCE.
又∵∠FDE=∠CDF,
∴△FDE∽△CDF,
![]()
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目