题目内容
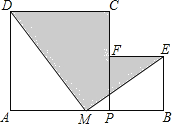
【题目】如图,在直角梯形ABCD中,∠A=90°,∠B=120°,AD= ![]() ,AB=6.在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°.
,AB=6.在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°. 
(1)当点E是AB的中点时,线段DF的长度是;
(2)若射线EF经过点C,则AE的长是 .
【答案】
(1)6
(2)2或5
【解析】解:(1.)如图1,过E点作EG⊥DF, 
∵E是AB的中点,
∴DG=3,
∴EG=AD= ![]() ,
,
∴∠DEG=60°,
∵∠DEF=120°,
∴tan60°= ![]() ,
,
解得GF=3,
∴DF=6;
(2.)如图2所示:
过点B作BH⊥DC,延长AB至点M,过点C作CM⊥AB于M,则BH=AD=MF= ![]() ,
,
∵∠ABC=120°,AB∥CD,
∴∠BCH=60°,
∴CH=BM= ![]() =
= ![]() =1,
=1,
设AE=x,则BE=6﹣x,
在Rt△EFM中,EF= ![]() =
= ![]() =
= ![]() ,
,
∵AB∥CD,
∴∠EFD=∠BEC,
∵∠DEF=∠B=120°,
∴△EDF∽△BCE,即△EDF∽△BFE
∴ ![]() ,
,
∴EF2=DFBE,即(7﹣x)2+3=7(6﹣x)
解得x=2或5
所以答案是:2或5.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对直角梯形的理解,了解一腰垂直于底的梯形是直角梯形.

【题目】为庆祝“六一”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校的人数多于乙校的人数,且甲校的人数不足90人)准备统一购买服装参加演出;下面是某服装厂给出的演出服装的价格表
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
(1)如果两所学校分别单独购买服装一共应付5000元,甲、乙两所学校各有多少学生准备参加演出?
(2)如果甲校有10名同学抽调去参加书法绘画比赛不能参加演出,请你为两所学校设计一种最省钱的购买服装方案.
【题目】问题背景:
小红同学在学习过程中遇到这样一道计算题“计算4×3.142﹣4×3.14×3.28+3.282”,他觉得太麻烦,估计应该有可以简化计算的方法,就去请教崔老师.崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
获取新知:
请你和小红一起完成崔老师提供的问题:
(1)填写下表:
x=﹣1,y=1 | x=1,y=0 | x=3,y=2 | x=1,y=1 | x=5,y=3 | |
A=2x﹣y | ﹣3 | 2 | 4 | 1 | 7 |
B=4x2﹣4xy+y2 | 9 | 4 |
|
|
|
(2)观察表格,你发现A与B有什么关系?
解决问题:
(3)请结合上述的有关信息,计算4×3.142﹣4×3.14×3.28+3.282.