题目内容
【题目】问题情境:
在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;
(应用):
(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .
(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .
(拓展):
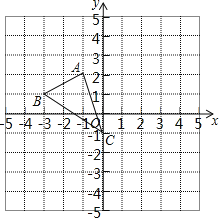
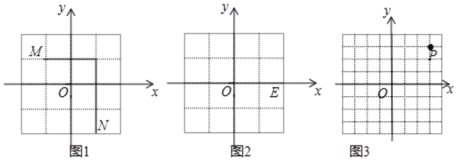
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
(1)已知E(2,0),若F(﹣1,﹣2),求d(E,F);
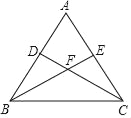
(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,求t的值;
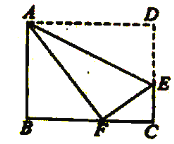
(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,求d(P,Q).
【答案】【应用】:(1)3;(2)(1,2)或(1,﹣2);【拓展】:(1)5;(2)t=±2;(3)d(P,Q)的值为4或8.
【解析】
(1)根据若y1=y2,则AB∥x轴,且线段AB的长度为|x1-x2|,代入数据即可得出结论;
(2)由CD∥y轴,可设点D的坐标为(1,m),根据CD=2即可得出|0-m|=2,解之即可得出结论;
【拓展】:(1)根据两点之间的折线距离公式,代入数据即可得出结论;
(2)根据两点之间的折线距离公式结合d(E,H)=3,即可得出关于t的含绝对值符号的一元一次方程,解之即可得出结论;
(3)由点Q在x轴上,可设点Q的坐标为(x,0),根据三角形的面积公式结合三角形OPQ的面积为3即可求出x的值,再利用两点之间的折线距离公式即可得出结论.
解:【应用】:
(1)AB的长度为|﹣1﹣2|=3.
故答案为:3.
(2)由CD∥y轴,可设点D的坐标为(1,m),
∵CD=2,
∴|0﹣m|=2,解得:m=±2,
∴点D的坐标为(1,2)或(1,﹣2).
【拓展】
:
(1)d(E,F)=|2﹣(﹣1)|+|0﹣(﹣2)|=5.
故答案为:5.
(2)∵E(2,0),H(1,t),d(E,H)=3,
∴|2﹣1|+|0﹣t|=3,
解得:t=±2.
(3)由点Q在x轴上,可设点Q的坐标为(x,0),
∵三角形OPQ的面积为3,
∴![]() |x|×3=3,解得:x=±2.
|x|×3=3,解得:x=±2.
当点Q的坐标为(2,0)时,d(P,Q)=|3﹣2|+|3﹣0|=4;
当点Q的坐标为(﹣2,0)时,d(P,Q)=|3﹣(﹣2)|+|3﹣0|=8
综上所述,d(P,Q)的值为4或8.