题目内容
【题目】如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点.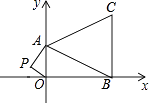
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点的坐标.
【答案】
(1)解:∵B(8,0),C(8,6),
∴BC=6,
∴S△ABC= ![]() ×6×8=24;
×6×8=24;
(2)解:∵A(0,4)(8,0),
∴OA=4,OB=8,
∴S四边形ABOP=S△AOB+S△AOP
= ![]() ×4×8+
×4×8+ ![]() ×4(﹣m)=16﹣2m,
×4(﹣m)=16﹣2m,
又∵S四边形ABOP=2S△ABC=48,
∴16﹣2m=48,
解得:m=﹣16,
∴P(﹣16,1).
【解析】(1)由点的坐标得出BC=6,即可求出△ABC的面积;
(2)求出OA=4,OB=8,由S四边形ABOP=S△AOB+S△AOP和已知条件得出方程,解方程即可.

练习册系列答案
相关题目