Question

【题目】在△ABC中，∠BAC＝90°，AB＝AC．

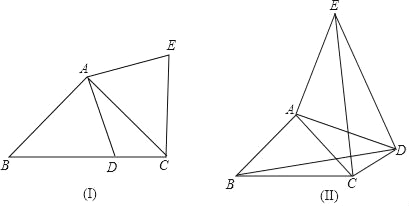
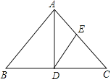
（I）如图，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到AE，连接EC．

求证：（1）△BAD≌△CAE；

（2）BC＝DC+EC．

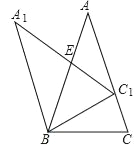
（Ⅱ）如图，D为△ABC外一点，且∠ADC＝45°，仍将线段AD绕点A逆时针旋转90°得到AE，连接EC，ED．

（1）△BAD≌△CAE的结论是否仍然成立？并请你说明理由；

（2）若BD＝9，CD＝3，求AD的长．

Answer 1

【答案】（I）（1）见解析；（2）见解析；（Ⅱ）（1）仍然成立；理由见解析（2）若AD＝6．

【解析】

（Ⅰ）（1）根据全等三角形的判定定理即可得到结论；

（2）根据全等三角形的性质即可得到结论；

（Ⅱ）（1）根据全等三角形的判定定理即可得到△BAD≌△CAE；

（2）根据全等三角形的性质得到BD＝CE＝9，根据勾股定理计算即可．

解：（Ⅰ）（1）∵∠BAC＝∠DAE＝90°，

∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE，

在△BAD和△CAE中，，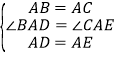

∴△BAD≌△CAE（SAS）；

（2）∵△BAD≌△CAE

∴BD＝CE，

∴BC＝BD+CD＝EC+CD；

（Ⅱ）（1）△BAD≌△CAE的结论仍然成立，

理由：∵将线段AD绕点A逆时针旋转90°得到AE，

∴△ADE是等腰直角三角形，

∴AE＝AD，

∵∠BAC+∠CAD＝∠DAE+∠CAD，

即∠BAD＝∠CAE，

在△BAD与△CAE中，，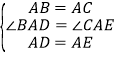

∴△BAD≌△CAE（SAS）；

（2）∵△BAD≌△CAE，

∴BD＝CE＝9，

∵∠ADC＝45°，∠EDA＝45°，

∴∠EDC＝90°，

∴DE＝＝6，

∵∠DAE＝90°，

∴AD＝AE＝DE＝6．