题目内容
【题目】把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG. 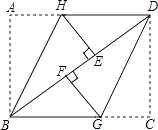
(1)求证:△BHE≌△DGF;
(2)若AB=6cm,BC=8cm,求线段FG的长.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠A=∠C=90°,∠ABD=∠BDC,
∵△BEH是△BAH翻折而成,
∴∠ABH=∠EBH,∠A=∠HEB=90°,AB=BE,
∵△DGF是△DGC翻折而成,
∴∠FDG=∠CDG,∠C=∠DFG=90°,CD=DF,
∴∠DBH= ![]() ∠ABD,∠BDG=
∠ABD,∠BDG= ![]() ∠BDC,
∠BDC,
∴∠DBH=∠BDG,
∴△BEH与△DFG中,
∠HEB=∠DFG,BE=DF,∠DBH=∠BDG,
∴△BEH≌△DFG
(2)解:∵四边形ABCD是矩形,AB=6cm,BC=8cm,
∴AB=CD=6cm,AD=BC=8cm,
∴BD= ![]() =
= ![]() =10,
=10,
∵由(1)知,FD=CD,CG=FG,
∴BF=10﹣6=4cm,
设FG=x,则BG=8﹣x,
在Rt△BGF中,
BG2=BF2+FG2,即(8﹣x)2=42+x2,解得x=3,即FG=3cm
【解析】(1)先根据矩形的性质得出∠ABD=∠BDC,再由图形折叠的性质得出∠ABH=∠EBH,∠FDG=∠CDG,∠A=∠HEB=90°,∠C=∠DFG=90°,进而可得出△BEH≌△DFG;(2)先根据勾股定理得出BD的长,进而得出BF的长,由图形翻折变换的性质得出CG=FG,设FG=x,则BG=8﹣x,再利用勾股定理即可求出x的值.
【考点精析】本题主要考查了勾股定理的概念和矩形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.

【题目】某检修小组从![]() 地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:
地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
![]() 求收工时,检修小组在
求收工时,检修小组在![]() 地的哪个方向?距离
地的哪个方向?距离![]() 地多远?
地多远?
![]() 在第几次纪录时距
在第几次纪录时距![]() 地最远?
地最远?
![]() 若汽车行驶每千米耗油
若汽车行驶每千米耗油![]() 升,问从
升,问从![]() 地出发,检修结束后再回到
地出发,检修结束后再回到![]() 地共耗油多少升?
地共耗油多少升?