题目内容
【题目】任何大于1的正整数m的三次幂均可分裂成m个连续奇数的和。如：23=3+5、33=7+9+11、43=13+15+17+19……依此规律，若m3分裂后其中有一个奇数是2019，则m的值是_____.
【答案】45
【解析】
观察可知,分裂成的奇数的个数与底数相同,然后求出到m3的所有奇数的个数的表达式,再求出奇数2019的是从3开始的第1009个数,然后确定出1009所在的范围即可得解
∵底数是2的分裂成2个奇数,底数为3的分裂成3个奇数,底数为4的分裂成4个奇数,
∴m
分裂成m个奇数,
所以,到m 的奇数的个数为
2+3+4+...+m=
∵2m+1=2019,n=1009,
∴奇数2019是从3开始的第1009个奇数
∵
第1009个奇数是底数为45的数的立方分裂的奇数的其中一个
即m=45
期末宝典单元检测分类复习卷系列答案
【题目】某年级共有150名女生，为了解该年级女生实心球成绩（单位：米）和一分钟仰卧起坐成绩（单位：个）的情况，从中随机抽取30名女生进行测试，获得了他们的相关成绩，并对数据进行整理、描述和分析．下面给出了部分信息．
a. 实心球成绩的频数分布表如下：
分组 |
|
|
|
|
|
|
频数 | 2 | m | 10 | 6 | 2 | 1 |
b. 实心球成绩在
这一组的是：
a7.0 7.0 7.0 7.1 7.1 7.1 7.2 7.2 7.3 7.3
c. 一分钟仰卧起坐成绩如下图所示：
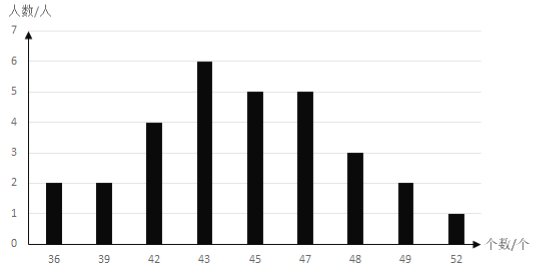
根据以上信息，回答下列问题：
（1） ①表中m的值为__________；
②一分钟仰卧起坐成绩的中位数为__________；
（2）若实心球成绩达到7.2米及以上时，成绩记为优秀．
①请估计全年级女生实心球成绩达到优秀的人数；
②该年级某班体育委员将本班在这次抽样测试中被抽取的8名女生的两项成绩的数据抄录如下：
女生代码 | A | B | C | D | E | F | G | H |
实心球 | 8.1 | 7.7 | 7.5 | 7.5 | 7.3 | 7.2 | 7.0 | 6.5 |
一分钟仰卧起坐 | * | 42 | 47 | * | 47 | 52 | * | 49 |
其中有3名女生的一分钟仰卧起坐成绩未抄录完整，但老师说这8名女生中恰好有4人两项测试成绩都达到了优秀，于是体育委员推测女生E的一分钟仰卧起坐成绩达到了优秀，你同意体育委员的说法吗？并说明你的理由．
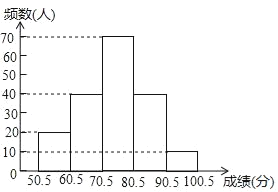
【题目】为在中小学生中普及交通法规常识，倡导安全出行，某市教育局在全市范围内组织七年级学生进行了一次“交规记心间”知识竞赛．为了解市七年级学生的竟赛成绩，随机抽取了若干名学生的竞赛成绩（成绩为整数，满分100分），进行统计后，绘制出如下频数分布表和如图所示的频数分布直方图（频数分布直方图中有一处错误）．
组别（单位：分） | 频数 | 频率 |
50.5～60.5 | 20 | 0.1 |
60.5～70.5 | 40 | 0.2 |
70.5～80.5 | 70 | b |
80.5～90.5 | a | 0.3 |
90.5～100.5 | 10 | 0.05 |
请根据图表信息回答下列问题：
（1）在频数分布表中，a＝ ，b＝ ．
（2）指出频数分布直方图中的错误，并在图上改正；
（3）甲同学说：“我的成绩是此次抽样调查所得数据的中位数”，问：甲同学的成绩应在什么范围？
（4）全市共有5000名七年级学生，若规定成绩在80分以上（不含80分）为优秀，估计这次竞赛中成绩为优秀的学生有多少人？
