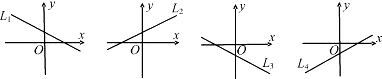题目内容
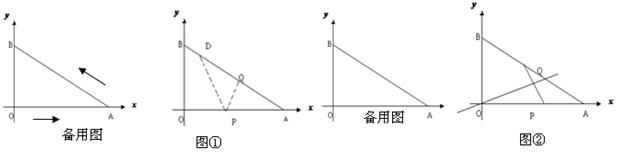
如图12-1,已知直线y= -x+4交x轴于点A,交y轴于点B.

(1)写出A、B两点的坐标分别是: ;
(2)设点P是射线y = x( )上一点,点P的横坐标为t,M是OP的中点(O是原点),以PM为对角线作正方形PDME.正方形PDME与△OAB公共部分的面积为S,求S与t之间的函数关系式,并求S的最大值.(图12-2、12-3供你探索问题时使用)
)上一点,点P的横坐标为t,M是OP的中点(O是原点),以PM为对角线作正方形PDME.正方形PDME与△OAB公共部分的面积为S,求S与t之间的函数关系式,并求S的最大值.(图12-2、12-3供你探索问题时使用)

(1)写出A、B两点的坐标分别是: ;
(2)设点P是射线y = x(
 )上一点,点P的横坐标为t,M是OP的中点(O是原点),以PM为对角线作正方形PDME.正方形PDME与△OAB公共部分的面积为S,求S与t之间的函数关系式,并求S的最大值.(图12-2、12-3供你探索问题时使用)
)上一点,点P的横坐标为t,M是OP的中点(O是原点),以PM为对角线作正方形PDME.正方形PDME与△OAB公共部分的面积为S,求S与t之间的函数关系式,并求S的最大值.(图12-2、12-3供你探索问题时使用)略
1)A(4,0),B(0,4); ……………………1分
(2)点P是射线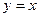 (
( )上一点,点P的横坐标为t
)上一点,点P的横坐标为t
∴点P坐标为(t,t) ……………………2分
令射线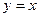 与直线
与直线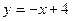 交于点N
交于点N
∴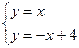 得
得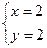
∵M为OP中点
∴M(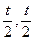 ) ……………………3分
) ……………………3分
∴D(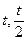 ),E(
),E(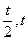 )
)
∵当点M(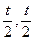 )在直线AB上时,
)在直线AB上时,
∴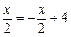 ,解得
,解得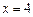 . ……………………4分
. ……………………4分
∵当点D(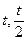 )在直线AB上时,(此时点E也在直线AB上)
)在直线AB上时,(此时点E也在直线AB上)
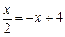 ,解得
,解得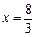 . ……………………5分
. ……………………5分
①当0<t≦2时,如图12-1此时正方形PDME与△OAB公共部分的面积为S即为正方形PDME的面积,
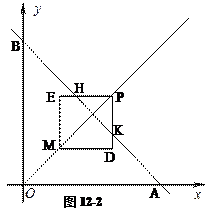 ∴
∴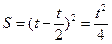 ……………………6分
……………………6分
∴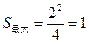 ……………………7分
……………………7分
②当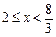 时,如图12-2直线AB分别与PE、PD有交点,
时,如图12-2直线AB分别与PE、PD有交点,
设交点分别为H、K,
此时,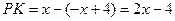 ,
,
又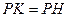 ,
,
∴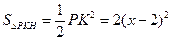 ,
,
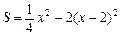
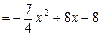
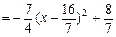 . ……………………8分
. ……………………8分
∵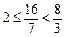 ,
,
∴当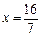 时,
时, . ……………………9分
. ……………………9分
③当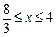 时,如图12-3,直线AB分别与ME、MD有交点,设交点分别为Q、G,
时,如图12-3,直线AB分别与ME、MD有交点,设交点分别为Q、G,
 ∴
∴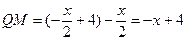 ,
,
又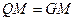 ,
,
∴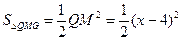 ,即
,即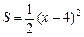 ……10分
……10分
∴当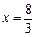 时,
时,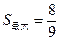 . ……………………11分
. ……………………11分
④当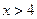 时,
时,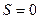 ……………………12分
……………………12分
综上得,当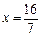 时,
时,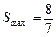 .
.
(2)点P是射线
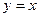 (
( )上一点,点P的横坐标为t
)上一点,点P的横坐标为t∴点P坐标为(t,t) ……………………2分
令射线
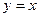 与直线
与直线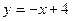 交于点N
交于点N∴
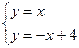 得
得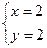
∵M为OP中点
∴M(
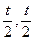 ) ……………………3分
) ……………………3分∴D(
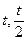 ),E(
),E(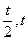 )
)∵当点M(
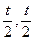 )在直线AB上时,
)在直线AB上时,∴
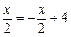 ,解得
,解得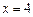 . ……………………4分
. ……………………4分∵当点D(
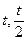 )在直线AB上时,(此时点E也在直线AB上)
)在直线AB上时,(此时点E也在直线AB上)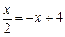 ,解得
,解得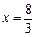 . ……………………5分
. ……………………5分①当0<t≦2时,如图12-1此时正方形PDME与△OAB公共部分的面积为S即为正方形PDME的面积,
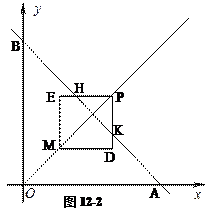 ∴
∴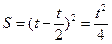 ……………………6分
……………………6分∴
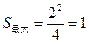 ……………………7分
……………………7分②当
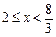 时,如图12-2直线AB分别与PE、PD有交点,
时,如图12-2直线AB分别与PE、PD有交点,设交点分别为H、K,
此时,
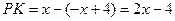 ,
,又
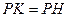 ,
,∴
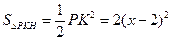 ,
,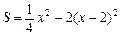
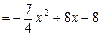
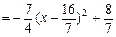 . ……………………8分
. ……………………8分∵
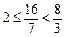 ,
,∴当
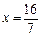 时,
时, . ……………………9分
. ……………………9分③当
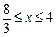 时,如图12-3,直线AB分别与ME、MD有交点,设交点分别为Q、G,
时,如图12-3,直线AB分别与ME、MD有交点,设交点分别为Q、G, ∴
∴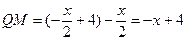 ,
,又
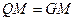 ,
,∴
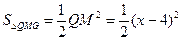 ,即
,即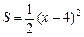 ……10分
……10分∴当
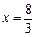 时,
时,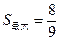 . ……………………11分
. ……………………11分④当
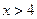 时,
时,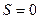 ……………………12分
……………………12分综上得,当
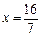 时,
时,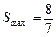 .
. 
练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目


 中y随
中y随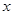 的增大而减小,则( )。
的增大而减小,则( )。 、
、
 、
、
 、
、
 、
、