题目内容
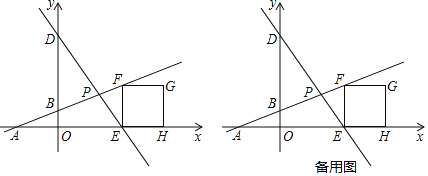
【题目】如图,在平面直角坐标系中,直线DE交x轴于点E(30,0),交y轴于点D(0,40),直线AB:y=![]() x+5交x轴于点A,交y轴于点B,交直线DE于点P,过点E作EF⊥x轴交直线AB于点F,以EF为一边向右作正方形EFGH.
x+5交x轴于点A,交y轴于点B,交直线DE于点P,过点E作EF⊥x轴交直线AB于点F,以EF为一边向右作正方形EFGH.
(1)求边EF的长;
(2)将正方形EFGH沿射线FB的方向以每秒![]() 个单位的速度匀速平移,得到正方形E1F1G1H1,在平移过程中边F1G1始终与y轴垂直,设平移的时间为t秒(t>0).
个单位的速度匀速平移,得到正方形E1F1G1H1,在平移过程中边F1G1始终与y轴垂直,设平移的时间为t秒(t>0).
①当点F1移动到点B时,求t的值;
②当G1,H1两点中有一点移动到直线DE上时,请直接写出此时正方形E1F1G1H1与△APE重叠部分的面积.
【答案】(1)EF=15;(2)①10;②120;
【解析】
(1)根据已知点E(30,0),点D(0,40),求出直线DE的直线解析式y=-![]() x+40,可求出P点坐标,进而求出F点坐标即可;
x+40,可求出P点坐标,进而求出F点坐标即可;
(2)①易求B(0,5),当点F1移动到点B时,t=10![]() ÷
÷![]() =10;
=10;
②F点移动到F'的距离是![]() t,F垂直x轴方向移动的距离是t,当点H运动到直线DE上时,在Rt△F'NF中,
t,F垂直x轴方向移动的距离是t,当点H运动到直线DE上时,在Rt△F'NF中,![]() =
=![]() ,EM=NG'=15-F'N=15-3t,在Rt△DMH'中,
,EM=NG'=15-F'N=15-3t,在Rt△DMH'中,![]() ,t=4,S=
,t=4,S=![]() ×(12+
×(12+![]() )×11=
)×11=![]() ;当点G运动到直线DE上时,在Rt△F'PK中,
;当点G运动到直线DE上时,在Rt△F'PK中,![]() =
=![]() ,PK=t-3,F'K=3t-9,在Rt△PKG'中,
,PK=t-3,F'K=3t-9,在Rt△PKG'中,![]() =
=![]() =
=![]() ,t=7,S=15×(15-7)=120.
,t=7,S=15×(15-7)=120.
(1)设直线DE的直线解析式y=kx+b,
将点E(30,0),点D(0,40),
∴![]() ,
,
∴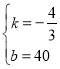 ,
,
∴y=﹣![]() x+40,
x+40,
直线AB与直线DE的交点P(21,12),
由题意知F(30,15),
∴EF=15;
(2)①易求B(0,5),
∴BF=10![]() ,
,
∴当点F1移动到点B时,t=10![]() =10;
=10;
②当点H运动到直线DE上时,
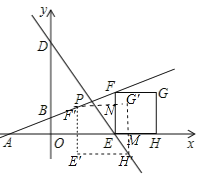
F点移动到F'的距离是![]() t,
t,
在Rt△F'NF中,![]() =
=![]() ,
,
∴FN=t,F'N=3t,
∵MH'=FN=t,
EM=NG'=15﹣F'N=15﹣3t,
在Rt△DMH'中,
![]() ,
,
∴![]() ,
,
∴t=4,
∴EM=3,MH'=4,
∴S=![]() ;
;
当点G运动到直线DE上时,
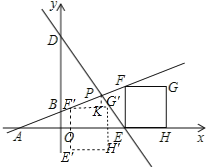
F点移动到F'的距离是![]() t,
t,
∵PF=3![]() ,
,
∴PF'=![]() t﹣3
t﹣3![]() ,
,
在Rt△F'PK中,
![]() ,
,
∴PK=t﹣3,F'K=3t﹣9,
在Rt△PKG'中,![]() =
=![]() =
=![]() ,
,
∴t=7,
∴S=15×(15﹣7)=120.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】立定跳远是体育中考选考项目之一,体育课上老师记录了某同学的一组立定跳远成绩如表:
成绩(m) | 2.3 | 2.4 | 2.5 | 2.4 | 2.4 |
则下列关于这组数据的说法,正确的是( )
A.众数是2.3B.平均数是2.4
C.中位数是2.5D.方差是0.01
【题目】从甲、乙两位运动员中选出一名参加在规定时间内的投篮比赛.预先对这两名运动员进行了6次测试,成绩如下(单位:个):
甲:6,12,8,12,10,12;
乙:9,10,11,10,12,8;
(1)填表:
平均数 | 众数 | 方差 | |
甲 | 10 |
|
|
乙 |
| 10 |
|
(2)根据测试成绩,请你运用所学的统计知识作出分析,派哪一位运动员参赛更好?为什么?