题目内容
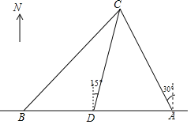
【题目】“仁爱礁”自古以来就是中国固有领海,也是中国渔民的传统渔场.为了维护我国渔民合法的海洋权益,每年我“渔政海巡船”都到“仁爱礁”进行护渔活动.如图,在岛礁东西方向上,有A,B两艘渔政船,现均收到我故障渔船C的求救信号.已知A,B两船相距90(![]() +1)海里,渔船C在船A的北偏西30°方向上,渔船C在船B的东北方向上,岛礁上有一观测点D,测得船C正好在观测点D的北偏东15°方向上
+1)海里,渔船C在船A的北偏西30°方向上,渔船C在船B的东北方向上,岛礁上有一观测点D,测得船C正好在观测点D的北偏东15°方向上
(1)分别求出AC和AD距离(若结果有根号,请保留根号);
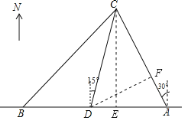
(2)已知距观测点D处110海里范围内有暗礁.为了及时营救渔船C,决定让海巡船A去营救,若海巡船A沿直线AC去营救,途中有无触暗礁危险?请说明理由:(参考数据:![]() ≈141,
≈141,![]() ≈1.73)
≈1.73)
【答案】(1)180,![]() ,;(2)途中没有触暗礁危险,理由见解析.
,;(2)途中没有触暗礁危险,理由见解析.
【解析】
(1)如图,作CE⊥AB于E,设AE=x海里,在Rt△AEC中,CE=AEtan60°=![]() x;在Rt△BCE中,BE=CE=
x;在Rt△BCE中,BE=CE=![]() x,求得x=90,求得AC=2x=180,CE=90
x,求得x=90,求得AC=2x=180,CE=90![]() ,过点D作DF⊥AC于点F,设AF=y,则DF=CF=
,过点D作DF⊥AC于点F,设AF=y,则DF=CF=![]() y,得AC=180,AD180(
y,得AC=180,AD180(![]() ﹣1);
﹣1);
(2)DF=![]() AF270﹣90
AF270﹣90![]() ≈114.3海里,故没有触暗礁危险.
≈114.3海里,故没有触暗礁危险.
解:(1)如图,作CE⊥AB于E,
由题意得:∠ABC=45°,∠BAC=60°,
设AE=x海里,
在Rt△AEC中,CE=AEtan60°=![]() x;
x;
在Rt△BCE中,BE=CE=![]() x.
x.
∴AE+BE=x+![]() x=90(
x=90(![]() +1),
+1),
解得:x=90.
∴AC=2x=180,CE=90![]() .
.
在△ACD中,∠DAC=60°,∠ADC=75°,则∠ACD=45°.
过点D作DF⊥AC于点F,
设AF=y,则DF=CF=![]() y,
y,
∴AC=y+![]() y=180,
y=180,
解得:y=90(![]() ﹣1),
﹣1),
∴AD=2y=180(![]() ﹣1).
﹣1).
答:A与C之间的距离AC为180海里,A与D之间的距离AD为180(![]() ﹣1)海里.
﹣1)海里.
(2)由(1)可知,DF=![]() AF=
AF=![]() ×90(
×90(![]() ﹣1)=270﹣90
﹣1)=270﹣90![]() ≈114.3海里,
≈114.3海里,
因为114.3>110,
所以巡逻船A沿直线AC航线,在去营救的途中没有触暗礁危险.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
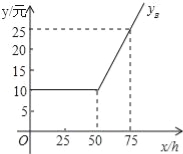
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?