题目内容
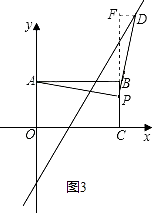
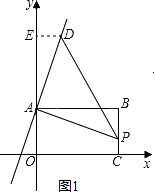
【题目】如图,矩形ABCO,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是两直线y1=2x+6、y2=2x﹣6中某条上的一点,若△APD是等腰Rt△,则点D的坐标为 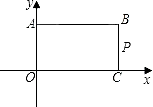
【答案】(4,2),(4,14),( ![]() ,
, ![]() ),(
),( ![]() ,
, ![]() )
)
【解析】解:易知:A(0,6),C(8,0),AB=8,OA=BC=6;
则点A正好位于直线y=2x+6上;
1)当点D位于直线y=2x+6上时,分三种情况:
①点P为直角顶点,结合图形,显然此时点D位于第四象限,不合题意;
②点D为直角顶点,那么∠DAP=45°,结合图形2可知:∠DAB>45°,
而点P位于线段BC上,故不存在这样的等腰直角三角形;
③点A为直角顶点,如图;
过D作DE⊥y轴于E,则△ADE≌△APB,得:AE=AB=8;
即点D的纵坐标为:14,代入y=2x+6中,可求得
点D(4,14);
2)当点D位于直线y=2x﹣6上时,分三种情况:
①点A为直角顶点,结合图形可知,此种情况显然不合题意;
②点D为直角顶点,分两种情况:
a、点D在矩形AOCB的内部时,过D作x轴的平行线EF,交直线OA于E,交直线BC于F,设D(x,2x﹣6);
则OE=2x﹣6,AE=6﹣(2x﹣6)=12﹣2x,DF=EF﹣DE=8﹣x;
则△ADE≌△DPF,得DF=AE,即:
12﹣2x=8﹣x,x=4;
∴D(4,2);
b、点D在矩形AOCB的外部时,设D(x,2x﹣6);
则OE=2x﹣6,AE=OE﹣OA=2x﹣6﹣6=2x﹣12,DF=EF﹣DE=8﹣x;
同1可知:△ADE≌△DPFAE=DF,即:
2x﹣12=8﹣x,x= ![]() ;
;
∴D( ![]() ,
, ![]() );
);
③点P为直角顶点,显然此时点D位于矩形AOCB的外部;
设点D(x,2x﹣6),则CF=2x﹣6,BF=2x﹣6﹣6=2x﹣12;
易证得△APB≌△PDF,得:
AB=PF=8,PB=DF=x﹣8;
故BF=PF﹣PB=8﹣(x﹣8)=16﹣x;
联立两个表示BF的式子可得:
2x﹣12=16﹣x,即x= ![]() ;
;
∴D( ![]() ,
, ![]() );
);
综合上面六种情况可得:存在符合条件的等腰直角三角形;
且D点的坐标为:(4,2),(4,14),( ![]() ,
, ![]() ),(
),( ![]() ,
, ![]() ).
).