题目内容
已知:如图,在 中,
中,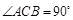 ,
, ,
, ,以
,以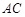 为直径的⊙O交
为直径的⊙O交 于点
于点 ,点
,点 是
是 的中点,OB,DE相交于点F。
的中点,OB,DE相交于点F。
【小题1】(1)求证: 是⊙O的切线;
是⊙O的切线;
【小题2】(2)求EF:FD的值。
【小题1】(1)证明:连结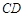 (如图), …………………… 1分
(如图), …………………… 1分
∵AC是⊙O的直径,
∴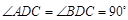 。
。 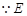 是
是 的中点,
的中点,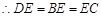 。
。
∴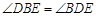
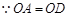 ,
, 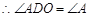 。
。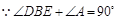 ,
,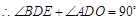 。
。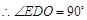 。
。
即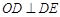 。
。
∵点D在⊙O上,
∴ 是⊙O的切线 。 ………………………………… 3分
是⊙O的切线 。 ………………………………… 3分
【小题2】(2)解:连结OE。
∵E是BC的中点,O是AC的中点,
∴OE∥AB,OE=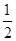 AB。
AB。
∴△OEF∽△BDF。
在 中,AC = 4,
中,AC = 4,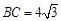 ,
,
根据勾股定理,得 AB= 8,
∴OE= 4,
∵sin∠ABC=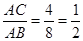 ,
,
∴∠ABC=30°。
∴∠A=60°。
∴  是边长为2的等边三角形。
是边长为2的等边三角形。
∴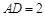 ,BD= AB-AD=6。
,BD= AB-AD=6。
∴EF:FD=OE:BD = 4:6=2:3 。 …… 5分
解析

练习册系列答案
相关题目
 中,
中, D是BC上的点,
D是BC上的点,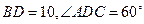 .求AC(
.求AC( ,结果保留整数).
,结果保留整数).
 中,
中, .
. ⊥
⊥ 于点
于点 ,且
,且 ,
, ⊥
⊥ 交
交 .求证:
.求证: .
.
 中,
中, 的角平分线
的角平分线 交
交 边于
边于 .
. 边上一点
边上一点 为圆心,过
为圆心,过 两点作
两点作 (不写作法,保留作图痕迹),再判断直线
(不写作法,保留作图痕迹),再判断直线 ,
, ,求线段
,求线段 与劣弧
与劣弧 所围成的图形面积.(结果保留根号和
所围成的图形面积.(结果保留根号和 )
)
 中,
中, 是
是 边上的高,
边上的高, 是
是 平分线。求
平分线。求 的度数
的度数