题目内容
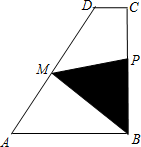 如图,梯形ABCD中,AB∥CD,AB⊥BC,M为AD中点,AB=2cm,BC=2cm,CD=0.5cm,点P在梯形的边上沿B?C?D?M运动,速度为1cm/s,则△BPM的面积ycm2与点P经过的路程xcm之间的函数关系用图象表示大致是下图中的( )
如图,梯形ABCD中,AB∥CD,AB⊥BC,M为AD中点,AB=2cm,BC=2cm,CD=0.5cm,点P在梯形的边上沿B?C?D?M运动,速度为1cm/s,则△BPM的面积ycm2与点P经过的路程xcm之间的函数关系用图象表示大致是下图中的( )A、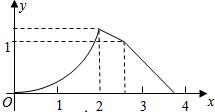 | B、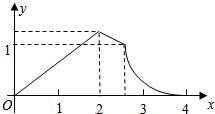 | C、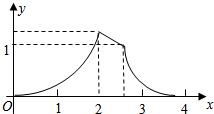 | D、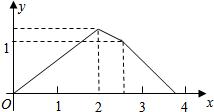 |
分析:根据题意,分3个阶段,①P在BC之间,②P在CD之间,③P在DM之间,分别分析△BMP的面积,可得答案.
解答:解:根据题意,分3个阶段;
①P在BC之间时,△BMP中,BP=x,为底,M到BC的距离,即中位线的长度为高,则高为
,有三角形的面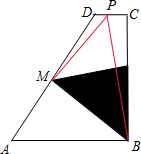 积公式可得,S=
积公式可得,S=
x;
②P在CD之间时,如右图所示,S=S梯形ABCD-S△ABM-S△PMD-S△PBC,可求得S=-0.5x+2.25,成一条线段;
③P在DM之间时,△BMP中,BM为底,P到BM的距离为高,有三角形的面积公式可得,S逐渐减小,且比②减小得快,是一条线段;
分析可得:D符合.
故选D.
①P在BC之间时,△BMP中,BP=x,为底,M到BC的距离,即中位线的长度为高,则高为
| 5 |
| 4 |
 积公式可得,S=
积公式可得,S=| 5 |
| 8 |
②P在CD之间时,如右图所示,S=S梯形ABCD-S△ABM-S△PMD-S△PBC,可求得S=-0.5x+2.25,成一条线段;
③P在DM之间时,△BMP中,BM为底,P到BM的距离为高,有三角形的面积公式可得,S逐渐减小,且比②减小得快,是一条线段;
分析可得:D符合.
故选D.
点评:本题主要考查动态问题的函数图象的知识点,解决此类问题,注意将过程分成几个阶段,依次分析各个阶段的变化情况,进而得到整体的变化情况.

练习册系列答案
相关题目
 已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )A、
| ||||
B、4
| ||||
C、
| ||||
D、4
|
 5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有
5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有 10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( )
10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( ) 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2, 如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.
如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.