题目内容
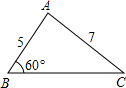 附加题:如图,在△ABC中,AB=5,AC=7,∠B=60°,求BC的长.(华东版教材实验区试题)
附加题:如图,在△ABC中,AB=5,AC=7,∠B=60°,求BC的长.(华东版教材实验区试题)
分析:可通过构建直角三角形来求解,过点A作AD⊥BC于D,AD是公共直角边,因此先求出AD是解题的关键,在Rt△ABD中,有AB的长,有∠B的度数,可以求出BD的长,AD的长,在Rt△ADC中,求出了AD的长,有AC的长,因此根据勾股定理可求出CD的长,有了BD、CD的长,也就求出了BC的长.
解答: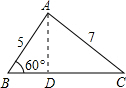 解:过点A作AD⊥BC于D,
解:过点A作AD⊥BC于D,
在Rt△ABD中,
AD=AB•sin60°=5×
=
,
BD=AB•cos60°=5×
=
,
在Rt△ADC中,
DC=
=
=
,
所以BC=BD+DC=8.
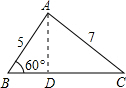 解:过点A作AD⊥BC于D,
解:过点A作AD⊥BC于D,在Rt△ABD中,
AD=AB•sin60°=5×
| ||
| 2 |
5
| ||
| 2 |
BD=AB•cos60°=5×
| 1 |
| 2 |
| 5 |
| 2 |
在Rt△ADC中,
DC=
| AC2-AD2 |
72-(
|
| 11 |
| 2 |
所以BC=BD+DC=8.
点评:在用解直角三角形的方法求线段长的时候,没有直角三角形的条件下,要根据已知条件构建直角三角形进行求解.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
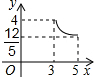
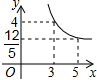
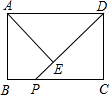 附加题:如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连接DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是( )
附加题:如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连接DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是( )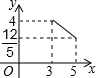
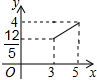
 27、附加题:
27、附加题: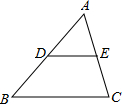 附加题:如图,在△ABC中,BC=2,则中位线DE=
附加题:如图,在△ABC中,BC=2,则中位线DE= 附加题:
附加题: (附加题)如图,在一块三角形区域土地ABC中,∠C=90°,AC=8,BC=6,底边AB上的高h=
(附加题)如图,在一块三角形区域土地ABC中,∠C=90°,AC=8,BC=6,底边AB上的高h=