题目内容
在平面直角坐标系中.过点P分別作x轴,y轴的垂线.与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.(1)判断点M(1,2),N(4,4)是否为和谐点? (2)若和谐点P(a,3)在直线y=-x+b(b为常数)上,则a,b的值为 。
M不是,N是 a=6 b=9
试题分析:M点与坐标轴的围成的图形,周长为(1+2)x2=6.面积为1x2="2" 两者不相等,所以不是和谐点。
同理可得N点与坐标轴的围成的图形周长为(4+4)x2=16,面积为4x4="16" ,两者相等,所以是和谐点。
P点与坐标轴的围成的图形周长为(a+3)x2="3a" 得a=6,又因为p点在直线y=-x+b上,代入得3="-6+b" 推出b=9
点评:该题有一定的难度,要求考试有较强的逻辑推理能力。做这类题型要注意数形结合的思想培养,在作图基础上列式举例归纳规律是解题关键

练习册系列答案
相关题目
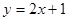 关于y轴对称。
关于y轴对称。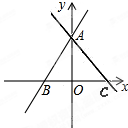
 与
与 轴,
轴, 轴分别相交于点
轴分别相交于点 .点
.点 从点
从点 出发沿射线
出发沿射线 以每秒1个单位长的速度匀速运动,同时点
以每秒1个单位长的速度匀速运动,同时点 从点
从点 出发沿
出发沿 以每秒1个单位长的速度向点
以每秒1个单位长的速度向点 匀速运动.当点
匀速运动.当点 ,
, 交
交 .记
.记 关于
关于 .设点
.设点 运动的时间是秒(
运动的时间是秒( ).
).
 时,则
时,则 = ,点
= ,点 时,若记四边形BDCO的面积为S,则求S关于的函数解析式
时,若记四边形BDCO的面积为S,则求S关于的函数解析式 为等腰直角三角形时,请直接写出的值
为等腰直角三角形时,请直接写出的值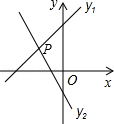




 是一次函数
是一次函数 的图象上的两个点,则
的图象上的两个点,则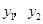 的大小关系是
的大小关系是


 分别作
分别作 轴,
轴, 轴的垂线,与坐标轴围成矩形
轴的垂线,与坐标轴围成矩形 的周长与面积相等,则点
的周长与面积相等,则点
 是否为和谐点,并说明理由;
是否为和谐点,并说明理由; 在直线
在直线 上,求点
上,求点 的值.
的值.