ЬтФПФкШн
ЃЈ2012•ШЊИлЧјжЪМьЃЉШчЭМЃЌAЁЂBЕФзјБъЗжБ№ЮЊЃЈ8ЃЌ4ЃЉЃЌЃЈ0ЃЌ4ЃЉЃЎЕуCДгдЕуOГіЗЂвдУПУы1ЕЅЮЛЕФЫйЖШбизХxжсЕФе§ЗНЯђдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtЃЈ0ЃМtЃМ5ЃЉЃЎЕуDдкxжсЩЯЃЌзјБъЮЊЃЈt+3ЃЌ0ЃЉЃЌЙ§ЕуDзїxжсЕФДЙЯпНЛABгкEЕуЃЌНЛOAгкGЕуЃЌСЌНгCEНЛOAгкЕуFЃЎ
ЃЈ1ЃЉЬюПеЃКCD=
ЃЈ2ЃЉЕБЁїEFGЕФУцЛ§ЮЊ
ЪБЃЌЕуGЧЁКУдкКЏЪ§y=
ЕквЛЯѓЯоЕФЭМЯѓЩЯЃЎЪдЧѓГіКЏЪ§y=
ЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЩшЕуQЕФзјБъЮЊЃЈ0ЃЌ2tЃЉЃЌЕуPдкЃЈ2ЃЉжаЕФКЏЪ§y=
ЕФЭМЯѓЩЯЃЌЪЧЗёДцдквдAЁЂCЁЂQЁЂPЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЪдЧѓГіЕуCЁЂPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
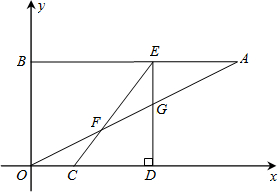
ЃЈ1ЃЉЬюПеЃКCD=
3
3
ЃЌCE=5
5
ЃЌAE=5-t
5-t
ЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉЃЛЃЈ2ЃЉЕБЁїEFGЕФУцЛ§ЮЊ
| 12 |
| 5 |
| k |
| x |
| k |
| x |
ЃЈ3ЃЉЩшЕуQЕФзјБъЮЊЃЈ0ЃЌ2tЃЉЃЌЕуPдкЃЈ2ЃЉжаЕФКЏЪ§y=
| k |
| x |

ЗжЮіЃКЃЈ1ЃЉгЩOC=tЃЌOD=t+3ЃЌМДПЩЧѓГіCDЕФГЄЃЛЯШгЩОиаЮЕФаджЪЕУГіDE=4ЃЌШЛКѓдкжБНЧЁїCDEжаЃЌдЫгУЙДЙЩЖЈРэМДПЩЧѓГіCEЕФГЄЃЛЯШгЩОиаЮЕФаджЪЕУГіBE=t+3ЃЌдйгЩAB=8МДПЩЧѓГіAEЕФГЄЃЛ
ЃЈ2ЃЉЙ§ЕуFзїFHЁЭDEгкHЃЌдђЁїEFGЕФУцЛ§=
EG•FHЃЎЯШдЫгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпOAЕФНтЮіЪНЃЌдйНЋGЕуЕФКсзјБъЃЈгыDЕуЕФКсзјБъЯрЕШЃЉДњШыЃЌЕУЕНGЕуЕФзнзјБъЃЌЧѓГіEGЕФГЄЃЛЯШгЩAEЁЮOCЃЌЕУГіЁїAEFЁзЁїOCFЃЌИљОнЯрЫЦШ§НЧаЮЖдгІБпГЩБШР§СаГіЕШЪНAEЃКOC=EFЃКCFЃЌЕУГіEF=5-tЃЌдйгЩе§ЯвКЏЪ§ЕФЖЈвхЕУГіFH=EF•sinЁЯCED=
ЃЌШЛКѓИљОнЁїEFGЕФУцЛ§ЮЊ
СаГіЙигкtЕФЗНГЬЃЌНтЗНГЬЧѓГіtЕФжЕЃЌЕУЕНGЕуЕФзјБъЮЊЃЈ4ЃЌ2ЃЉЃЌдђдЫгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіЙ§GЕуЕФЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЕБвдAЁЂCЁЂQЁЂPЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЪБЃЌЪзЯШИљОнетЫФИіЕуЕФЮЛжУМА0ЃМtЃМ5ЃЌХаЖЯЦНааЫФБпаЮПЩФмЪЧ?APCQЛђ?APQCЃЌдйгЩЦНааЫФБпаЮЕФЖдНЧЯпЛЅЯрЦНЗжЕФаджЪЕУГіСНЖдНЧЯпЕФжаЕужиКЯЃЎЩшPЃЈxЃЌ
ЃЉЃЌИљОнжаЕузјБъЙЋЪНСаГіЙигкxЁЂtЕФЗНГЬзщЃЌНтЗНГЬзщМДПЩЃЎ
ЃЈ2ЃЉЙ§ЕуFзїFHЁЭDEгкHЃЌдђЁїEFGЕФУцЛ§=
| 1 |
| 2 |
| 3(5-t) |
| 5 |
| 12 |
| 5 |
ЃЈ3ЃЉЕБвдAЁЂCЁЂQЁЂPЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЪБЃЌЪзЯШИљОнетЫФИіЕуЕФЮЛжУМА0ЃМtЃМ5ЃЌХаЖЯЦНааЫФБпаЮПЩФмЪЧ?APCQЛђ?APQCЃЌдйгЩЦНааЫФБпаЮЕФЖдНЧЯпЛЅЯрЦНЗжЕФаджЪЕУГіСНЖдНЧЯпЕФжаЕужиКЯЃЎЩшPЃЈxЃЌ
| 8 |
| x |
НтД№ЃКНтЃКЃЈ1ЃЉЁпгЩЬтвтЃЌПЩжЊOC=tЃЌOD=t+3ЃЌ
ЁрCD=OD-OC=t+3-t=3ЃЛ
дкжБНЧЁїCDEжаЃЌЁпЁЯCDE=90ЁуЃЌCD=3ЃЌDE=OB=4ЃЌ
ЁрCE=
=5ЃЛ
ЁпAB=8ЃЌBE=OD=t+3ЃЌ
ЁрAE=AB-BE=8-ЃЈt+3ЃЉ=5-tЃЎ
ЙЪД№АИЮЊ3ЃЌ5ЃЌ5-tЃЛ
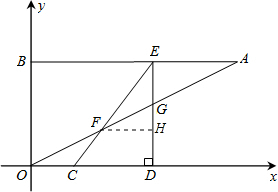 ЃЈ2ЃЉШчЭМЃЌЙ§ЕуFзїFHЁЭDEгкHЃЌдђЁїEFGЕФУцЛ§=
ЃЈ2ЃЉШчЭМЃЌЙ§ЕуFзїFHЁЭDEгкHЃЌдђЁїEFGЕФУцЛ§=
EG•FHЃЎ
ЁпOЃЈ0ЃЌ0ЃЉЃЌAЃЈ8ЃЌ4ЃЉЃЌ
ЁржБЯпOAЕФНтЮіЪНЮЊy=
xЃЌ
ЕБx=t+3ЪБЃЌy=
ЃЌЁрGЃЈt+3ЃЌ
ЃЉЃЌ
ЁрEG=DE-DG=4-
=
ЃЎ
ЁпAEЁЮOCЃЌ
ЁрЁїAEFЁзЁїOCFЃЌ
ЁрAEЃКOC=EFЃКCFЃЌМДЃЈ5-tЃЉЃКt=EFЃКЃЈ5-EFЃЉЃЌ
НтЕУEF=5-tЃЌ
ЁрFH=EF•sinЁЯCED=ЃЈ5-tЃЉЁС
=
ЃЌ
ЁрЁїEFGЕФУцЛ§=
EG•FH=
ЁС
ЁС
=
ЃЌ
ЁпЁїEFGЕФУцЛ§ЮЊ
ЃЌ
Ёр
=
ЃЌ
НтЕУt=1Лђ9ЃЌ
Ёп0ЃМtЃМ5ЃЌ
Ёрt=1ЃЌ
ЁрGЃЈ4ЃЌ2ЃЉЃЎ
ЁпЕуGдкКЏЪ§y=
ЕквЛЯѓЯоЕФЭМЯѓЩЯЃЌ
Ёрk=4ЁС2=8ЃЎ
ЙЪЫљЧѓКЏЪ§ЕФНтЮіЪНЮЊy=
ЃЛ
ЃЈ3ЃЉЕБЕуQЕФзјБъЮЊЃЈ0ЃЌ2tЃЉЃЌЕуPдкЃЈ2ЃЉжаЕФКЏЪ§y=
ЕФЭМЯѓЩЯЪБЃЌДцдквдAЁЂCЁЂQЁЂPЮЊЖЅЕуЕФЦНааЫФБпаЮЃЌРэгЩШчЯТЃК
ЗжСНжжЧщПіЃКЩшPЃЈxЃЌ
ЃЉЃЎ
ЂйЕБЫФБпаЮAPCQЪЧЦНааЫФБпаЮЪБЃЌдђACгыPQЛЅЯрЦНЗжЃЌМДACЕФжаЕугыPQЕФжаЕужиКЯЃЎ
ЁпAЃЈ8ЃЌ4ЃЉЃЌCЃЈtЃЌ0ЃЉЃЌQЃЈ0ЃЌ2tЃЉЃЌ
Ёр
ЃЌ
НтЕУ
ЃЌ
ЃЈЩсШЅЃЉЃЌ
ЁрCЃЈ
-3ЃЌ0ЃЉЃЌPЃЈ5+
ЃЌ10-2
ЃЉЃЎ
ЂкЕБЫФБпаЮAPQCЪЧЦНааЫФБпаЮЪБЃЌдђAQгыCPЛЅЯрЦНЗжЃЌМДAQЕФжаЕугыCPЕФжаЕужиКЯЃЎ
ЁпAЃЈ8ЃЌ4ЃЉЃЌCЃЈtЃЌ0ЃЉЃЌQЃЈ0ЃЌ2tЃЉЃЌ
Ёр
ЃЌ
НтЕУ
ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЎ
злЩЯПЩжЊЃЌЫљЧѓCЕуЕФзјБъЮЊЃЈ
-3ЃЌ0ЃЉЃЌPЕуЕФзјБъЮЊЃЈ5+
ЃЌ10-2
ЃЉЃЎ
ЁрCD=OD-OC=t+3-t=3ЃЛ
дкжБНЧЁїCDEжаЃЌЁпЁЯCDE=90ЁуЃЌCD=3ЃЌDE=OB=4ЃЌ
ЁрCE=
| CD2+DE2 |
ЁпAB=8ЃЌBE=OD=t+3ЃЌ
ЁрAE=AB-BE=8-ЃЈt+3ЃЉ=5-tЃЎ
ЙЪД№АИЮЊ3ЃЌ5ЃЌ5-tЃЛ
 ЃЈ2ЃЉШчЭМЃЌЙ§ЕуFзїFHЁЭDEгкHЃЌдђЁїEFGЕФУцЛ§=
ЃЈ2ЃЉШчЭМЃЌЙ§ЕуFзїFHЁЭDEгкHЃЌдђЁїEFGЕФУцЛ§=| 1 |
| 2 |
ЁпOЃЈ0ЃЌ0ЃЉЃЌAЃЈ8ЃЌ4ЃЉЃЌ
ЁржБЯпOAЕФНтЮіЪНЮЊy=
| 1 |
| 2 |
ЕБx=t+3ЪБЃЌy=
| t+3 |
| 2 |
| t+3 |
| 2 |
ЁрEG=DE-DG=4-
| t+3 |
| 2 |
| 5-t |
| 2 |
ЁпAEЁЮOCЃЌ
ЁрЁїAEFЁзЁїOCFЃЌ
ЁрAEЃКOC=EFЃКCFЃЌМДЃЈ5-tЃЉЃКt=EFЃКЃЈ5-EFЃЉЃЌ
НтЕУEF=5-tЃЌ
ЁрFH=EF•sinЁЯCED=ЃЈ5-tЃЉЁС
| 3 |
| 5 |
| 3(5-t) |
| 5 |
ЁрЁїEFGЕФУцЛ§=
| 1 |
| 2 |
| 1 |
| 2 |
| 5-t |
| 2 |
| 3(5-t) |
| 5 |
| 3(5-t)2 |
| 20 |
ЁпЁїEFGЕФУцЛ§ЮЊ
| 12 |
| 5 |
Ёр
| 3(5-t)2 |
| 20 |
| 12 |
| 5 |
НтЕУt=1Лђ9ЃЌ
Ёп0ЃМtЃМ5ЃЌ
Ёрt=1ЃЌ
ЁрGЃЈ4ЃЌ2ЃЉЃЎ
ЁпЕуGдкКЏЪ§y=
| k |
| x |
Ёрk=4ЁС2=8ЃЎ
ЙЪЫљЧѓКЏЪ§ЕФНтЮіЪНЮЊy=
| 8 |
| x |
ЃЈ3ЃЉЕБЕуQЕФзјБъЮЊЃЈ0ЃЌ2tЃЉЃЌЕуPдкЃЈ2ЃЉжаЕФКЏЪ§y=
| k |
| x |
ЗжСНжжЧщПіЃКЩшPЃЈxЃЌ
| 8 |
| x |
ЂйЕБЫФБпаЮAPCQЪЧЦНааЫФБпаЮЪБЃЌдђACгыPQЛЅЯрЦНЗжЃЌМДACЕФжаЕугыPQЕФжаЕужиКЯЃЎ
ЁпAЃЈ8ЃЌ4ЃЉЃЌCЃЈtЃЌ0ЃЉЃЌQЃЈ0ЃЌ2tЃЉЃЌ
Ёр
|
НтЕУ
|
|
ЁрCЃЈ
| 21 |
| 21 |
| 21 |
ЂкЕБЫФБпаЮAPQCЪЧЦНааЫФБпаЮЪБЃЌдђAQгыCPЛЅЯрЦНЗжЃЌМДAQЕФжаЕугыCPЕФжаЕужиКЯЃЎ
ЁпAЃЈ8ЃЌ4ЃЉЃЌCЃЈtЃЌ0ЃЉЃЌQЃЈ0ЃЌ2tЃЉЃЌ
Ёр
|
НтЕУ
|
|
злЩЯПЩжЊЃЌЫљЧѓCЕуЕФзјБъЮЊЃЈ
| 21 |
| 21 |
| 21 |
ЕуЦРЃКБОЬтПМВщСЫЗДБШР§КЏЪ§ЕФзлКЯЬтЃЌЦфжаЩцМАЕНЕФжЊЪЖЕугаОиаЮЕФаджЪЁЂКЏЪ§НтЮіЪНЕФЧѓЗЈЁЂШ§НЧаЮЕФУцЛ§ЁЂЦНааЫФБпаЮЕФаджЪЕШЃЌЪЧИїЕижаПМЕФШШЕуКЭФбЕуЃЌНтЬтЪБзЂвтЪ§аЮНсКЯКЭЗжРрЬжТлЕШЪ§бЇЫМЯыЕФдЫгУЃЌЭЌбЇУЧвЊМгЧПбЕСЗЃЌЪєгкжаЕЕЬтЃЎ

СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП
 ЃЈ2012•ШЊИлЧјжЪМьЃЉШчЭМЃЌаЁИеАбвЛИіАыОЖЮЊ12cmЕФдВаЮгВжНЦЌЕШЗжГЩШ§ИіЩШаЮЃЌгУЦфжавЛИіЩШаЮжЦзїГЩвЛИідВзЖаЮЕФжНУБЃЈЯЮНгДІЮоЗьЯЖЧвВЛжиЕўЃЉЃЌдђдВзЖаЮжНУБЕФЕзУцдВЕФАыОЖЪЧ
ЃЈ2012•ШЊИлЧјжЪМьЃЉШчЭМЃЌаЁИеАбвЛИіАыОЖЮЊ12cmЕФдВаЮгВжНЦЌЕШЗжГЩШ§ИіЩШаЮЃЌгУЦфжавЛИіЩШаЮжЦзїГЩвЛИідВзЖаЮЕФжНУБЃЈЯЮНгДІЮоЗьЯЖЧвВЛжиЕўЃЉЃЌдђдВзЖаЮжНУБЕФЕзУцдВЕФАыОЖЪЧ ЃЈ2012•ШЊИлЧјжЪМьЃЉЃЈ1ЃЉМЦЫуЃК
ЃЈ2012•ШЊИлЧјжЪМьЃЉЃЈ1ЃЉМЦЫуЃК