题目内容
已知,如图,AB为半圆O的直径,C为OB上一点,OC:CB=1:3,DC⊥AB交半圆O于D,过D作半圆O的切线交AB的延长线于E.
(1)若BE=12,求半圆O的半径长;
(2)在弧BD上任取一点P(不与B、D重合),连接EP 并延长交弧AD于F,设PC=x,EF=y,求y关于x的函数关系式,并指出自变量x的取值范围.
并延长交弧AD于F,设PC=x,EF=y,求y关于x的函数关系式,并指出自变量x的取值范围.
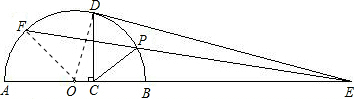 解:(1)连接OD,
解:(1)连接OD,设OC=a,则BC=3a,OD=OB=4a;
∵DE是半圆的切线,
∴OD⊥DE;
又∵DC⊥AB,
∴△OCD∽△ODE,
∴OD2=OC×OE,
(4a)2=a×(4a+12),
解得a=0(不合题意,舍去),a=1,
∴OB=4a=4.
(2)连接OF;
∵△DCE∽△ODE,
∴DE:OE=CE:DE,
∴DE2=OE×EC;
由切割线定理可得DE2=PE×EF,
∴OE×EC=PE×EF,
∴PE:CE=OE:FE;
∵∠CEP=∠FEO,
∴△CEP∽△FEO,
∴PC:OF=EC:EF,
x:4=15:y,
∴y=
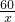 ;
;当P取B点时,PC最短,此时PC=3;
当P取D点时,PC最长,此时PC=
 ;
;∴3<x<
 .
.分析:(1)是求线段的长,由于题目中给出了两条线段长度的比,所以可以设未知数,利用图形的几何性质构造方程来求解.
(2)涉及研究线段与线段函数关系的问题,线段作为变量,解题的关键是用几何定理揭示它们之间的等量关系,列出方程后,再化为函数解析式.实质上还是构造方程,利用方程思想解题.
点评:此例是利用相似三角形对应边成比例的性质为等量关系,列出方程后,再化为函数解析式的.特别要注意用图形的几何性质来确定自变量的取值范围.

练习册系列答案
相关题目


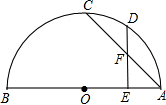 已知:如图,AB为⊙O的直径,C、D是半圆弧上的两点,E是AB上除O外的一点,AC与DE相交于F.①
已知:如图,AB为⊙O的直径,C、D是半圆弧上的两点,E是AB上除O外的一点,AC与DE相交于F.① =
= =
=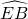 ,∠BOE=55°,则∠AOC的度数为________度.
,∠BOE=55°,则∠AOC的度数为________度.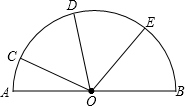
 =
= =
= ,∠BOE=55°,则∠AOC的度数为 度.
,∠BOE=55°,则∠AOC的度数为 度.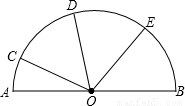
 ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.