题目内容
△ABC中，AB=AC，D是BC中点，DE⊥AB于E，DF⊥AC于F，求证：DE=DF．
证明：∵AB=AC，D是BC中点，
∴∠ABC=∠ACB，BD=DC．
∵DE⊥AB于E，DF⊥AC于F，
∴∠DEB=∠DFC=90°
在△DEB和△DFC中，
，
∴△DEB≌△DFC（AAS），
∴DE=DF．
分析：根据AB=AC，D是BC中点，DE⊥AB于E，DF⊥AC于F，利用角角边定理可证此题，
点评：此题主要考查学生对全等三角形的判定与性质和等腰三角形的性质的理解和掌握，难度不大，是一道基础题．
∴∠ABC=∠ACB，BD=DC．
∵DE⊥AB于E，DF⊥AC于F，
∴∠DEB=∠DFC=90°
在△DEB和△DFC中，
，∴△DEB≌△DFC（AAS），
∴DE=DF．
分析：根据AB=AC，D是BC中点，DE⊥AB于E，DF⊥AC于F，利用角角边定理可证此题，
点评：此题主要考查学生对全等三角形的判定与性质和等腰三角形的性质的理解和掌握，难度不大，是一道基础题．
练习册系列答案
春雨教育同步作文系列答案
相关题目
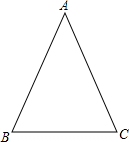如图，在△ABC中，AB=AC，∠A=36°，
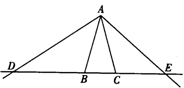15、如图，在△ABC中，AB=AC，点D，E在直线BC上运动．如果∠DAE=l05°，△ABD∽△ECA，则∠BAC=
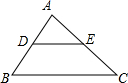△ABC中，AB=AC，D、E分别是AB、AC的中点，若AB=4，BC=6，则△ADE的周长是
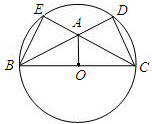，连接AO、BE、DC．