Question

【题目】已知抛物线的顶点是C（0，a）（a＞0，a为常数），并经过点（2a，2a），点D（0，2a）为一定点．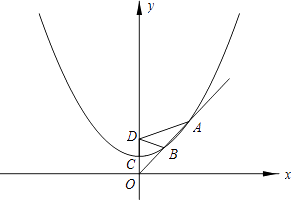

（1）求含有常数a的抛物线的解析式；
（2）设点P是抛物线上任意一点，过P作PH丄x轴．垂足是H，求证：PD=PH；
（3）设过原点O的直线l与抛物线在笫一象限相交于A、B两点，若DA=2DB．且S△ABD=4 ．求a的值．

Answer 1

【答案】
（1）

解：设抛物线的解析式为y=kx2+a，

∵经过点（2a，2a），

4a2k+a=2a，

∴k= ，

则抛物线的解析式为：y= x2+a

（2）

解：连接PD，设抛物线上一点P（x，y），过P作PH⊥x轴，PG⊥y轴，

在Rt△GDP中，由勾股定理得：PD2=DG2+PG2=（y﹣2a）2+x2=y2﹣4ay+4a2+x2，

∵y= x2+a，

∴x2=4a×（y﹣a）=4ay﹣4a2，

∴PD2=y2﹣4ay+4a2+4ay﹣4a2=y2=PH2，

∴PD=PH

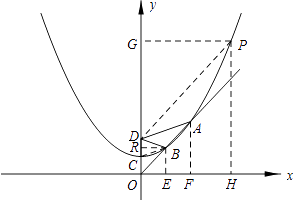
（3）

解：过B作BE⊥x，AF⊥x，

由（2）的结论：BE=DB，AF=DA，

∵DA=2DB，

∴AF=2BE，

∴AO=2OB，

∴B是OA的中点，

∵C是OD的中点，

连接BC，∴BC= = =BE=DB，

过B作BR⊥y轴，

∵BR⊥CD，

∴CR=DR，OR=a+ = ，

∴ = x2+a，

∴x2=2a2，

∵x＞0，

∴x= a，

∴B（ a， ），AO=2OB，

∴S△OBD=S△ABD=4 ，

∴ ×2a× a=4 ，

∴a2=4，

∵a＞0，

∴a=2

【解析】（1）根据抛物线的图象假设出解析式为y=kx2+a，将经过点（2a，2a），代入求出即可；（2）根据勾股定理得出PD2=DG2+PG2 ， 进而求出PD=PH；（3）利用（2）中结论得出BE=DB，AF=DA，即可得出B是OA的中点，进而得出S△OBD=S△ABD=4 ，即可得出a的值．
【考点精析】根据题目的已知条件，利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．