Question

在平面直角坐标系中，给定以下五点A（-2，0）、B（1，0）、C（4，0）、D（-2，

9

2

）、E（0，-6）．从这五点中选取三点，使经过这三点的抛物线满足对称轴平行于y轴．
我们约定：把经过三点A、E、B的抛物线表示为抛物线AEB．
（1）问符合条件的抛物线还有哪几条？不求解析式，请用约定的方法一一表示出来；
（2）在（1）中是否存在这样的一条抛物线，它与余下的两点所确定的直线不相交？如果存在，试求出抛物线及直线的解析式并证明；如果不存在，请说明理由．

Answer 1

分析：（1）根据经过不在一条直线上的三个点，就可以作出一条抛物线分别得出即可．
（2）根据待定系数法就可以求出抛物线的解析式，即可得出存在抛物线DBC，它与直线AE不相交．

解答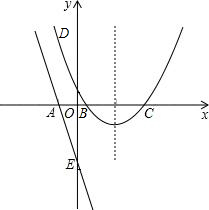：解：（1）符合条件的抛物线还有5条，分别如下：
①抛物线AEC；
②抛物线CBE；
③抛物线DEB；
④抛物线DEC；
⑤抛物线DBC．

（2）在（1）中存在抛物线DBC，它与直线AE不相交．
设抛物线DBC的解析式为y=ax²+bx+c，
将D（-2，

9

2

），B（1，0），C（4，0）三点坐标分别代入，
得：4a-2b+c=

9

2

，a+b+c=0，
即16a+4b+c=0，
解这个方程组，得：a=

1

4

，b=-

5

4

，c=1，
∴抛物线DBC的解析式为y=

1

4

x²-

5

4

x+1．
另法：设抛物线为y=a（x-1）（x-4），代入D（-2，

9

2

），得a=

1

4

也可．
又设直线AE的解析式为y=mx+n．将A（-2，0），E（0，-6）两点坐标分别代入，
得：-2m+n=0，n=-6．
解这个方程组，得m=-3，n=-6．
∴直线AE的解析式为y=-3x-6．

点评：此题主要考查了待定系数法求函数的解析式，已知不在同一直线上的三点就可以确定一条抛物线，待定系数法求二次函数解析式是中考中考查重点，同学们应熟练掌握此知识．