题目内容
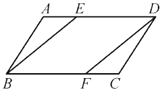
【题目】如图,在□ABCD中,点E,F分别在AD,BC边上,且AE=CF.求证:
(1)△ABE≌△CDF;
(2)四边形BFDE是平行四边形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由四边形ABCD是平行四边形,根据平行四边形的对边相等,对角相等,即可证得∠A=∠C,AB=CD,又由AE=CF,利用SAS,即可判定△ABE≌△CDF;
(2)由四边形ABCD是平行四边形,根据平行四边形对边平行且相等,即可得AD∥BC,AD=BC,又由AE=CF,即可证得DE=BF,然后根据对边平行且相等的四边形是平行四边形,即可证得四边形BFDE是平行四边形.
试题解析:(1)∵四边形ABCD是平行四边形,
∴∠A=∠C,AB=CD,
在△ABE和△CDF中,
∵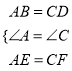 ,
,
∴△ABE≌△CDF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴AD-AE=BC-CF,
即DE=BF,
∴四边形BFDE是平行四边形.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
【题目】某校男子篮球队20名队员的身高如表:则此男子排球队20名队员身高的中位数是( )
身高(cm) | 170 | 176 | 178 | 182 | 198 |
人数(个) | 4 | 6 | 5 | 3 | 2 |
A.176cm
B.177cm
C.178cm
D.180cm