题目内容
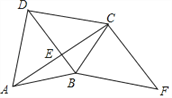
【题目】如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠CDB=45°,BD=2,求AC的长.
【答案】(1)证明见解析;(2)AC=2![]() .
.
【解析】整体
(1)证明四边形DBCF的两组对边分别平行;(2)作CM⊥BF于F,△CFM是等腰直角三角形,求出CM的长即可得到AC的长.
解:(1)证明:∵AC⊥BD,∠FCA=90°,∠CBF=∠DCB.
∴BD∥CF,CD∥BF,
∴四边形DBFC是平行四边形;
(2)解:∵四边形DBFC是平行四边形,
∴CF=BD=2,∠F=∠CDB=45°,
∵AB=BC,AC⊥BD,∴AE=CE,
作CM⊥BF于F,
∵BC平分∠DBF,∴CE=CM,
∴△CFM是等腰直角三角形,
∴CM=![]() CF=
CF=![]() ,∴AE=CE=
,∴AE=CE=![]() ,
,
∴AC=2![]() .
.


练习册系列答案
相关题目
【题目】下表中有两种移动电话计费方式:
月使用费(元) | 主叫限定时间(分钟) | 主叫超时费(元/分钟) | 被叫 | |
方式一 | 65 | 160 | 0.25 | 免费 |
方式二 | 100 | 380 | 0.19 | 免费 |
说明:月使用费固定收取,主叫不超限定时间不再收费,主叫超时部分加收超时费;被叫免费.
(1)若李杰某月主叫通话时间为200分钟则他按方式一计费需 元,按方式二计费需 元;若他按方式二计费需103.8元,则主叫通话时间为 分钟;
(2)是否存在某主叫通话时间t(分钟),按方式一和方式二的计费相等,若存在,请求出t的值;若不存在,请说明理由;
(3)请你通过计算分析后,直接给出当月主叫通话时间t(分钟)满足什么条件时,选择方式一省钱;当每月主叫通话时间t(分钟)满足什么条件时,选择方式二省钱.