Question

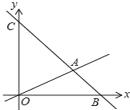
【题目】已知在平面直角坐标系xOy中，O是坐标原点，如图1，直角三角板△MON中，OM=ON=，OQ=1，直线l过点N和点N，抛物线y=ax2+x+c过点Q和点N．

（1）求出该抛物线的解析式；

（2）已知点P是抛物线y=ax2+x+c上的一个动点．

①初步尝试

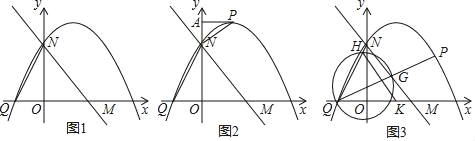
若点P在y轴右侧的该抛物线上，如图2，过点P作PA⊥y轴于点A，问：是否存在点P，使得以N、P、A为顶点的三角形与△ONQ相似．若存在，求出点P的坐标，若不存在，请说明理由；

②深入探究

若点P在第一象限的该抛物线上，如图3，连结PQ，与直线MN交于点G，以QG为直径的圆交QN于点H，交x轴于点R，连结HR，求线段HR的最小值．

Answer 1

【答案】（1）y=﹣x2+x+（2）①（1，）、（3，0）、（5，﹣4）②

【解析】

（1）根据待定系数法可求抛物线解析式；

（2）①分三种情况，情况一：点P在第一象限时，△APN∽△ONQ，情况二：点P恰好在x轴上，情况三：P在第四象限内，进行讨论可求出点P的坐标；

②连结CH和CR，得到HR最小时，只需要半径最小，即直径最小即可．用面积法求出QG=，进一步得到HR最小值．

（1）由题意可知，Q（﹣1，0），N（0，），

∴c=，即y=ax2+x+，

将Q（﹣1，0）代入解析式得0=a﹣+，解得a=﹣，

∴抛物线解析式是y=﹣x2+x+；

（2）①分三种情况，如图2，

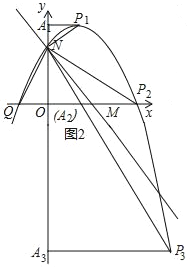
情况一：点P在第一象限时，△APN∽△ONQ，

设AN=m，则AP=m，

则P的坐标（m，m+），

而点P在抛物线上，代入可得m+=﹣（m）2++（m）+，

解得m=，

∴P1（1，）；

情况二：点P恰好在x轴上，P2（3，0），

情况三：P在第四象限内，同情况一方法可解得

P3（5，﹣4），

②连结CH和CR，如图3，

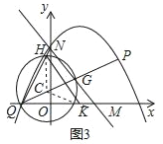
∵∠NQ0=60°，

∴∠HCR=120°，

∵CH=CR，

∴HR=CH，

∴HR最小时，只需要半径最小，即直径最小即可，

∴过Q作NM的垂线，垂直时，QG最小，

∴用面积法求出，QG=，

HR最小值=．