题目内容
一个三位数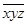 (其中,x、y、z互不相等),将其各个数位的数字重新排列,分别得到的最大数和最小数仍是三位数,若所得到的最大三位数与最小三位数之差是原来的三位数,则这个三位数是 .
(其中,x、y、z互不相等),将其各个数位的数字重新排列,分别得到的最大数和最小数仍是三位数,若所得到的最大三位数与最小三位数之差是原来的三位数,则这个三位数是 .
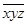 (其中,x、y、z互不相等),将其各个数位的数字重新排列,分别得到的最大数和最小数仍是三位数,若所得到的最大三位数与最小三位数之差是原来的三位数,则这个三位数是 .
(其中,x、y、z互不相等),将其各个数位的数字重新排列,分别得到的最大数和最小数仍是三位数,若所得到的最大三位数与最小三位数之差是原来的三位数,则这个三位数是 .495;
试题分析:一个三位数
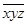 (其中,x、y、z互不相等),将其各个数位的数字重新排列,分别得到的最大数和最小数仍是三位数,可知x、y、z三个数不等于零。根据题意,由于不知道x、y、z三个数大小关系,
(其中,x、y、z互不相等),将其各个数位的数字重新排列,分别得到的最大数和最小数仍是三位数,可知x、y、z三个数不等于零。根据题意,由于不知道x、y、z三个数大小关系,重新设组成三位数的三个数字是a,b,c,且a>b>c,则最大的三位数是a×100+b×10+c,最小的三位数是c×100+b×10+a,
所以差是(a×100+b×10+c)-(c×100+b×10+a)=99×(a-c).
所以原来的三位数是99的倍数,可能的取值有198,297,396,495,594,693,792,891,
其中只有495符合要求,954-459=495.
则原来的x=4,y=9,z=5.这个三位数是495.
点评:本题难度中等,主要考查学生对位置原则知识点的掌握。假设组成三位数的三个数字是a,b,c,且a>b>c,则最大的三位数是a×100+b×10+c,最小的三位数是c×100+b×10+a.为解题关键。.

练习册系列答案
相关题目

 =__________________.
=__________________.



 ,则ab=
,则ab=