题目内容
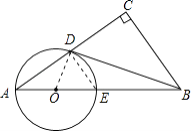
【题目】如图,在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
(1)求证:直线BD与⊙O相切;
(2)若AD:AE= ![]() :
: ![]() ,BC=6,求切线BD的长.
,BC=6,求切线BD的长.
【答案】
(1)证明:连接OD
∵OA=OD,
∴∠A=∠ADO(等边对等角).
又∵∠A+∠CDB=90°(已知),
∴∠ADO+∠CDB=90°(等量代换),
∴∠ODB=180°﹣(∠ADO+∠CDB)=90°,即BD⊥OD.
又∵OD是圆O的半径.
∴BD是⊙O切线
(2)解:连接DE,则∠ADE=90°(圆周角定理).
∵∠C=90°,
∴∠ADE=∠C,
∴DE∥BC,
又∵D是AC中点,
∴DE是△ABC的中位线,
∴DE= ![]() BC=3,AE=BE.
BC=3,AE=BE.
∵AD:AE= ![]() :
: ![]() ,
,
在直角△ADE中,利用勾股定理求得AE=3 ![]() ,则AB=6
,则AB=6 ![]() .
.
∴BD2=ABBE=6 ![]() ×3
×3 ![]() =54,
=54,
∴BD=3 ![]() .
.
【解析】(1)要证明BD是⊙O切线,由题意可知点D在圆上,因此连接OD,需证OD⊥BD,就要证∠ODB=90°,根据已知易证∠ADO+∠CDB=90°,即可证得结论
(2)先证明DE∥BC,由D是AC中点,可证得DE是△ABC的中位线,即可求得DE的长,再根据AD与AE的比值及勾股定理,就可以求得AE、AB的长,然后根据切割线定理得出BD2=ABBE,从而可求得BD的长。
【考点精析】掌握勾股定理的概念和三角形中位线定理是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.

练习册系列答案
相关题目







