Question

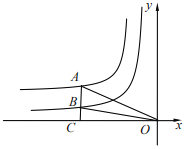
【题目】如图，点A是反比例图数y＝（x＜0）图象上一点，AC⊥x轴于点C，与反比例函数y＝（x＜0）图象交于点B，AB＝2BC，连接OA、OB，若△OAB的面积为3，则m+n＝（　　）

A.﹣4B.﹣6C.﹣8D.﹣12

Answer 1

【答案】D

【解析】

利用反比例函数比例系数k的几何意义得到S△AOC=|m|=-m，S△BOC=|n|=-n，利用AB=2BC得到S△ABO=2S△OBC=3，所以-n=，解得n=-3，再利用-m=3+得m=-9，然后计算m+n的值．

解:∵AC⊥x轴于点C，与反比例函数y＝（x＜0）图象交于点B，

而m＜0，n＜0，

∴S△AOC＝|m|＝﹣m，S△BOC＝|n|＝﹣n，

∵AB＝2BC，

∴S△ABO＝2S△OBC＝3，

即﹣n＝，解得n＝﹣3

∵﹣m＝3+，解得m＝﹣9，

∴m+n＝﹣9﹣3＝﹣12．

故选：D．